Použití metody TFM (Total Focusing Method) s funkcí obálky
Nicolas Badeau1 Guillaume Painchaud-April1 Alain Le Duff1
1Olympus NDT Canada
3415 Rue Pierre-Ardouin
Quebec QC, G1P 0B3
Shrnutí
Tento dokument představuje postup při výpočtu obálky snímku získávaného metodou TFM (Total Focusing Method) a výhody používání této obálky TFM jako součásti řešení, které je ve shodě s příslušnými předpisy a normami. Obálka TFM je získávána normalizovaným vypočítáváním dvou rozdílných snímků TFM, jmenovitě prvního snímku TFM vypočítávaného za použití standardně získávaného záznamu s dokonalou maticí (FMC) a druhého snímku TFM vypočítávaného za použití záznamu FMC zpracovávaného Hilbertovou transformací. Výsledný snímek s obálkou TFM poskytuje lepší základ pro použití metody amplitudového určování velikostí, jelikož je odolnější proti kolísání amplitudy ve srovnání se standardním oscilačním snímkem TFM získaným při totožném rastrovém rozlišení. Oproti standardnímu oscilačnímu snímku TFM je proto pro obálku TFM možno nastavovat hrubší rozlišení rastru, a tudíž zároveň snižovat celkovou náročnost výpočtu a v konečném důsledku zvyšovat výslednou rychlost pořizování snímku.
Úvod
Metoda TFM představuje nedávno zavedený a uznaný postup nedestruktivního hodnocení materiálů a struktur. Určité předpisy a normy již nyní obsahují oddíly týkající se záznamu s dokonalou maticí (FMC) a metody TFM při nedestruktivním zkoušení (NDT) [1], [2].
Některá zařízení pro nedestruktivní zkoušení, jako například detektor vad OmniScan™ X3, umožňují zobrazování za použití metody TFM v reálném čase. Postup využívající metodu TFM společně se způsobem záznamu FMC je souhrnně popsán v následující části dokumentu, avšak základní předpoklad spočívá v tom, že metoda TFM je založena na získávání součtu většího počtu hodnot amplitud měřených elementárním amplitudovým snímáním. Snímky TFM jsou snímky oscilačního typu, protože zvuková vlna má původ v elementárním amplitudovém snímání. Charakterizační schémata, které se nacházejí v aplikacích pro nedestruktivní zkoušení, naproti tomu v zásadě představují amplitudové postupy, u kterých lze oscilační chování považovat za nadbytečný akustický artefakt. Běžný postup, který je v praxi používán k přizpůsobení oscilačního chování charakterizačním schématům, spočívá v usměrňování amplitudy tak, aby získávaný obraz měl přísně kladné hodnoty. I když tento přístup může být použitelný k usnadnění interpretace obrazu ve vztahu k jeho plně oscilačnímu protějšku, v tomto dokumentu bude popsáno, jak může použití obálky signálu dále zlepšit výsledky získávané charakterizací a skutečně zvýšit rychlost pořizování záznamů oproti standardnímu oscilačnímu snímku TFM.
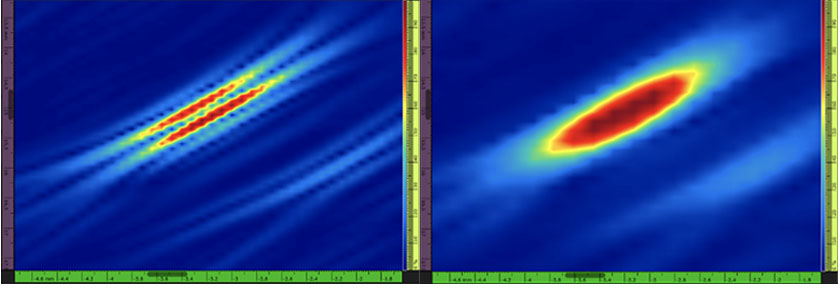
Obrázek 1 – Vlevo: příklad snímku TFM postranního vrtaného otvoru (SDH) s přísně kladnými hodnotami amplitud a oscilací signálu (tj. standardního snímku TFM). Rozlišení rastru činí 0,08 mm (λ / 8,1) a maximální amplituda činí 108,7 %. Vpravo: snímek přesně téhož prvku SDH při použití obálky TFM. Rozlišení rastru činí 0,16 mm (λ / 4,0) a maximální amplituda činí 122,6 %.
Použití takového oscilačního snímku TFM je spojeno s několika nevýhodami. První nevýhodou je to, že rozlišení rastru TFM, tj. vzdálenost mezi dvěma pixely ve snímku, musí činit přibližně λ / 8, aby bylo ve shodě s předpisy [1]–[3]. V tomto článku je λ vlnová délka, která je ve vztahu s centrální frekvencí sondy a rychlostí šíření zvuku v součásti. Malé rozlišení rastru je spojeno s vysokou náročností výpočtů, což má za bezprostřední následek nižší rychlost pořizování snímků. U oscilačních snímků TFM je rovněž nepříznivě ovlivňována odolnost proti kolísání amplitudy, která je u metod amplitudového určování velikostí vad nezbytná. Maximální amplituda měřeného odrazu zvuku je ve skutečnosti silně závislá na fázovém posunu získávaného signálu.
Všechny tyto problémy je možno vyřešit použitím obálky TFM, jelikož tato obálka odstraňuje kmitání signálu v obrazu a umožňuje provádění odolnějšího měření maximální amplitudy (viz Obrázek 1). Použití obálky TFM přináší prospěch v podobě vyšší produktivity při pořizování záznamů, jelikož vyžaduje snížené rozlišení rastru – tj. větší rozestup mezi dvěma sousedními pixely – při stejné odolnosti proti kolísání amplitudy ve srovnání se standardním snímkem TFM. Při použití obálky TFM je například postačující rozlišení rastru činící přibližně λ / 4 k získání stejné stálosti amplitudy (2 dB) jako u standardního oscilačního snímku TFM pořizovaného za použití rozlišení λ / 8 [3].
Cílem tohoto dokumentu je poskytnout specialistům z oboru nedestruktivního zkoušení informace o přednostech používání obálky TFM. Nejprve uvedeme souhrnnou rekapitulaci metody FMC-TFM, která bude následována krátkým představením koncepcí souvisejících s vypočítáváním obálky TFM. Na závěr představíme výhody používání obálky TFM jako součásti řešení ve shodě s předpisy a normami, a to ve srovnání se standardními snímky TFM oscilačního typu.
Souhrnné informace o metodě FMC-TFM
Typickým znakem ultrazvukového fázového pole je schopnost zaostřování v kterémkoli požadovaném místě kontrolovaného dílu. Postup zaostřování fázového pole využívá jednotlivých zpoždění – jak při vysílání, tak i při příjmu – k synchronizování časů průchodu krátkých impulzních signálů v oblasti zájmu. V ohniskové zóně vzorku se zmenšuje celková šířka generovaného akustického svazku a výrazně zvyšuje odpovídající rozlišení při detekci [4]–[12].
Metoda TFM představuje přirozené rozšíření této schopnosti, jelikož vytváří zaostřený svazek prostřednictvím fokalizace fázového pole a jeho usměrňování v každém místě celé oblasti zájmu kontrolovaného dílu, přičemž operátor sleduje pouze sadu fokalizovaných datových bodů ve vysokém rozlišení [13]–[16]. Oblast zájmu často sestává ze stejnoměrného kartézského rastru obsahujícího všechny požadované cílové objekty postupu fokalizace. Dosahování této fokalizace v každém místě rastru za použití konvenčního postupu fyzického utváření svazků by zjevně bylo mimořádně časově náročné vzhledem k době fyzického šíření zvukových vln, která je potřebná k dosažení každého místa v oblasti zájmu.
Jelikož typické ultrazvukové vlny používané při nedestruktivním zkoušení jsou lineární, fyzické utváření svazků, které je pro všechny zúčastněné prvky dané apertury výsledkem superpozice skutečných akustických polí, může být emulováno za použití postupu následné akvizice, který je založen na datové sadě získávané při provádění záznamu s dokonalou maticí (FMC). Získávání datové sady FMC vyžaduje zaznamenávání signálu pocházejícího od všech prvků tvořících přijímající aperturu v době, kdy jsou akustické emise vytvářeny každým jednotlivým prvkem tvořícím vysílající aperturu. Samotná datová sada FMC je pak tvořena velkým množstvím elementárních amplitudových snímků zahrnujícím všechny kombinace vysílajících i přijímajících prvků.
Stejně, jako je tomu u konvenčního zaostřeného fázového pole, vyžaduje získávání fokalizované amplitudy v daných fokalizačních místech splnění následujících předpokladů:
- vypočítávání doby průchodu potřebné k šíření zvukových vln tak, aby bylo umožněno dosahování polohy ohniska shodující se se zvolenou polohou oblasti zájmu v rastru i následné odesílání těchto vln zpět k přijímajícímu prvku, a to pro všechny dvojice vysílajících a přijímajících prvků tvořících příslušnou aperturu,
- výběr datového bodu amplitudy odpovídajícího příslušné celé době průchodu během vysílání i přijímání, a to rovněž pro všechny dvojice vysílajících a přijímajících prvků tvořících příslušnou aperturu,
- vytváření součtu všech vybraných datových bodů amplitudy příslušejících všem zúčastněným prvkům tvořícím vysílající i přijímající apertury,
- umísťování výsledné součtové amplitudy v počáteční vybrané poloze uvnitř rastru.
Opakování těchto kroků pro všechna místa rastru v celé oblasti zájmu pak vytváří amplitudovou mapu pro všechny hodnoty amplitud odpovídající fokalizovanému svazku, a to jak při vysílání, tak i při příjmu. Tento způsob využívání dat FMC k vytváření mapy amplitud fokalizovaných v každém z míst celé oblasti zájmu (tj. v zóně TFM) je pak označováno jako metoda FMC-TFM.
Jak se provádí výpočet obálky TFM
Tato část dokumentu popisuje způsob vypočítávání obálky TFM za použití stejných elementárních amplitudových snímků (FMC), jaké jsou získávány při použití standardní metody TFM. Je třeba poukázat na skutečnost, že obálka má fyzickou podobu, a nepředstavuje tedy pouhý algoritmus vyhlazování obrazu. Obálka snímku TFM má svůj původ v jednotlivých amplitudových snímcích, ze kterých sestává. Nejprve bude koncepce obálky představena, za účelem schematického znázornění jejího chování, pomocí Gaussovy řady časových impulzů. Proces je aplikován také na empirický amplitudový snímek a na úplný snímek TFM.
Signál a(t) odpovídá získanému signálu – tj. ekvivalentu elementárního amplitudového snímku pořízeného prostřednictvím záznamu typu FMC – a ve skutečnosti je reálnou součástí komplexního analytického signálu z(t), který může být zapsán jako
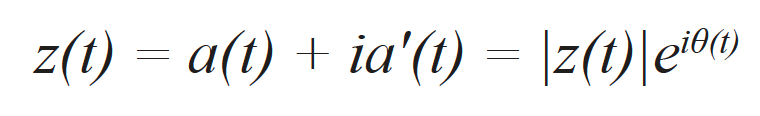
kde a’(t) odpovídá pomyslné části analytického signálu a θ(t) je okamžitá fáze signálu. Pomyslná část byla účinně vypočítána za použití Hilbertovy transformace [17]. Obálka signálu odpovídá normalizovanému analytickému signálu, což je možno zapsat jako
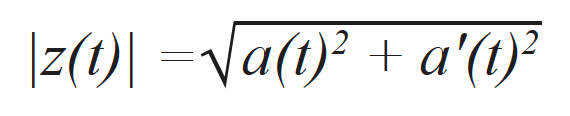
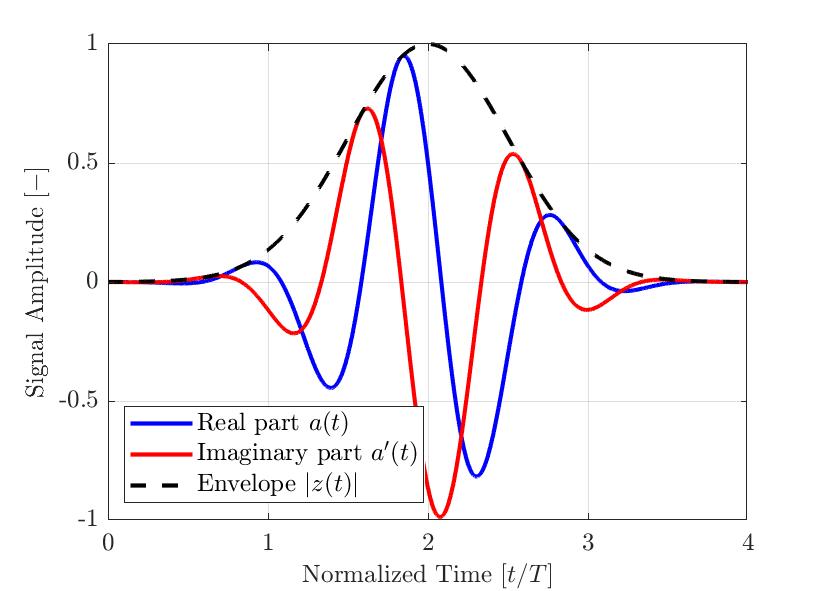
Obrázek 2 – Typický impulz modulovaný pomocí Gaussovy řady a určený pro použití v oblasti nedestruktivního zkoušení. Znázorněny jsou skutečný a pomyslný díl společně s vypočítanou obálkou. Časová osa je normalizována pomocí vybrané periody centrální frekvence impulzu.
Obrázek 2 znázorňuje příklad jednoduchého impulzu a(t) modulovaného pomocí Gaussovy řady. Skutečný signál a(t) je znázorněn modře, jeho pomyslná část a’(t) transformovaná Hilbertovou metodou je znázorněna červeně a výsledná obálka |z(t)| je znázorněna přerušovanou čarou. Z výše uvedené rovnice je zřejmé, že obálka signálu |z(t)| není ovlivňována okamžitou fází θ(t) tohoto signálu. Signály s rozdílnými fázovými posunutími ϕ tudíž mohou mít stejnou obálku. Obrázek 3 znázorňuje několik impulzů modulovaných pomocí Gaussovy řady s rozdílnými fázovými posunutími ϕ, společně s jejich výslednou obálkou. Měřená maximální amplituda signálu je tudíž při použití obálky signálu odolnější než absolutní hodnota skutečné složky analytického signálu.
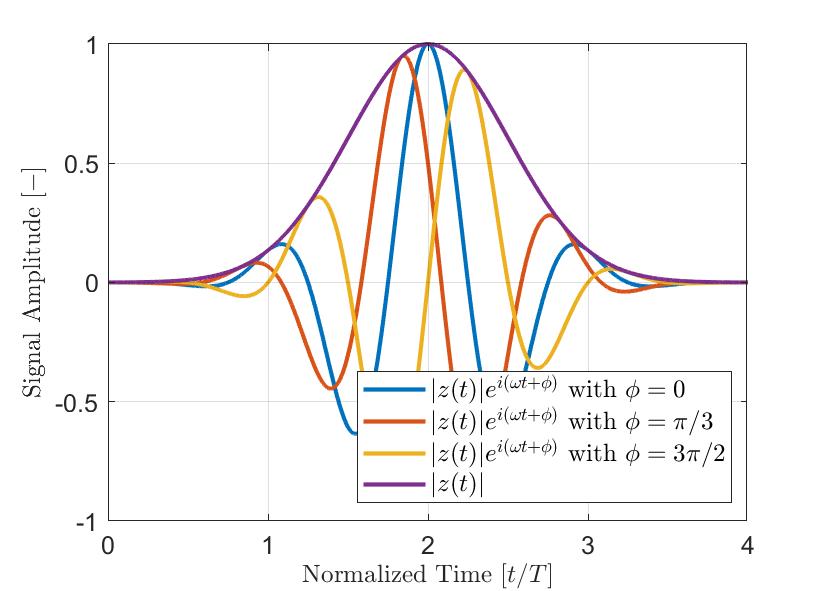
Obrázek 3 – Typické impulzy (|z(t)|ei(ωt+ϕ)) modulované pomocí Gaussovy řady s rozdílnými fázovými posunutími ϕ. Obálka |z(t)| signálů je zřetelně nezávislá na okamžité fázi analytického signálu.
Stejný postup je možno použít k získání obálky empirického amplitudového snímku. Obrázek 4 znázorňuje typický elementární amplitudový snímek pořízený prostřednictvím FMC a Obrázek 5 znázorňuje tentýž amplitudový snímek (modrý) společně s jeho Hilbertovou transformací (červená) a vypočítanou obálkou (přerušovaná čára). Všechny znázorněné signály jsou normalizovány podle maxima amplitudové obálky.
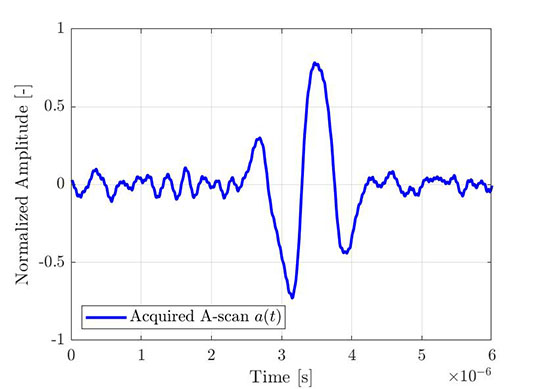 Obrázek 4 – Část pořízeného elementárního amplitudového snímku (ze záznamu FMC) | 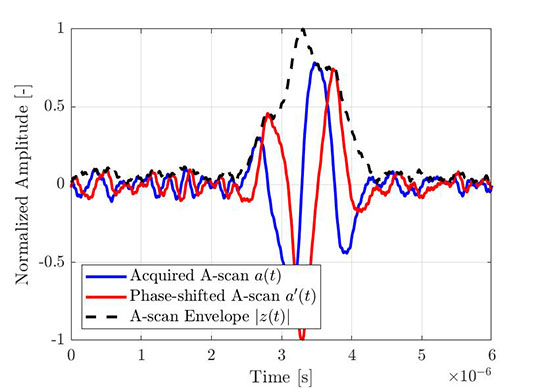 Obrázek 5 – Stejný elementární amplitudový snímek společně s jeho Hilbertovou transformací a vypočítanou obálkou |
Obraz s obálkou TFM – s jednotlivými indexy bodů rastru (k,l) – se vypočítává za použití analytických signálů příslušejících všem amplitudovým snímkům, které se na vytváření tohoto obrazu podílejí [15]. Ve skutečnosti se jedná o výsledek výpočtu normalizovaného analytického obrazu TFM y(k,l) sestávajícího ze standardního snímku TFM x(k,l) vypočítaného za použití standardních pořízených dat FMC a ze snímku TFM x'(k,l) vypočítaného pomocí Hilbertovy transformace dat FMC. V obou případech je použita stejná sada zpoždění. Obálka TFM je pak vypočítána za použití následujícího výrazu
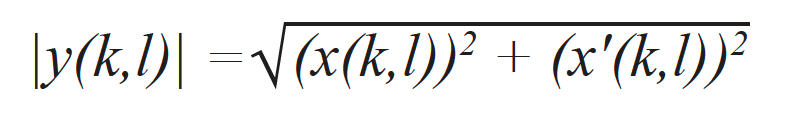
Obraz s obálkou TFM je proto výsledkem kombinace dvou obrazů TFM (viz obrázek 6): jednoho získaného z reálné složky tvořené elementárními amplitudovými snímky a druhého získaného z vypočítané pomyslné složky elementárních amplitudových snímků. I když tento postup zvyšuje náročnost výpočtu a snižuje rychlost pořizování záznamu nedestruktivním zkušebním přístrojem, v další části dokumentu názorně předvedeme, že potřebné rozlišení rastru lze významně snížit i bez nepříznivého ovlivnění stálosti amplitudy, čímž je umožněno opětovné zvýšení rychlosti pořizování záznamu, která je pak vyšší než při použití standardních snímků TFM.
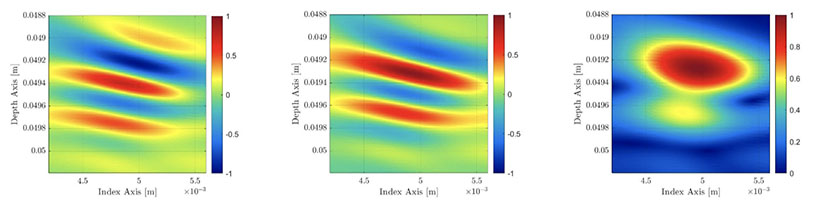
Obrázek 6 – Vlevo: standardní snímek TFM (nikoli v absolutní hodnotě). Uprostřed: snímek TFM vypočítaný za použití Hilbertovy transformace záznamu FMC. Vpravo: výsledný obraz s obálkou TFM.
Výhody použití obálky TFM
V této části dokumentu jsou názorně předvedeny výhody obálky TFM, a to na základě vzájemného porovnání několika snímků TFM s rozdílnými poměry rozlišení rastru, které se pohybují v rozsahu od λ / 9,3 do λ / 4,0, a sledování prováděného za použití různé kritické kontrolní metriky. Výsledky byly získány za použití sondy 5L32-A31 a optického klínu SA31-N55S-IHC při pozorování ocelového bloku opatřeného postranním vrtaným otvorem (SDH) o průměru 1 mm (viz Obrázek 7). Mezi optickým klínem a ocelovým blokem byl použit vazební gel (Sonotech Ultragel II). Data byla pořízena za použití detektoru vad Olympus OmniScan™ X3. Byla vybrána akustická dráha typu impulz–ozvěna (T-T), přičemž velikost oblasti činila (20 mm × 20 mm). Vlnová délka přiřazená dílu a vybrané akustické dráze činila λ = 0,648 mm. Rozlišení rastru bylo zaznamenáváno v jednotkách představujících zlomky vlnové délky.

Obrázek 7 – Fotografie uspořádání použitého k pořízení snímků TFM uvedených v Tabulce 1. Modrý obdélník odpovídá celé oblasti zájmu (20 mm × 20 mm) a červený obdélník odpovídá přiblížené oblasti zájmu (5 mm × 5 mm) obsažené ve snímcích zobrazených v Tabulce 1. Použili jsme sondu 5L32-A31 a optický klín SA31-N55S-IHC. Ocelový blok má tloušťku 40 mm.
Tabulka 1 zobrazuje výsledné snímky TFM pro rozdílné hodnoty rozlišení rastru v rozsahu od λ / 9,3 do λ / 4,0, a to jak pro standardní snímky TFM, tak i pro snímky TFM s obálkou. V každém ze snímků TFM je vyznačena vypočítaná hodnota [3] stálosti amplitudy i výsledná rychlost pořizování záznamu.
Rozlišení rastru | Standardní snímek TFM | Snímek s obálkou TFM |
|---|---|---|
λ / 9,3 | 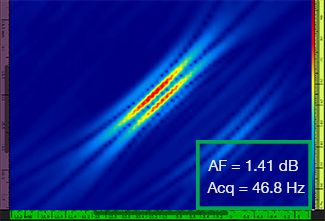 | 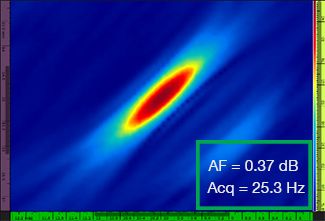 |
λ / 8,1 | 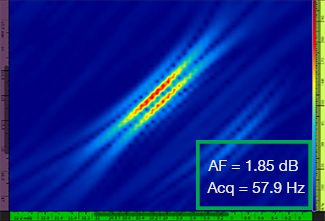 | 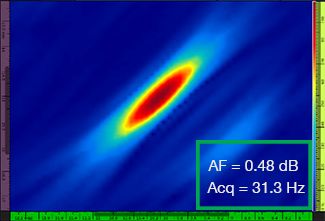 |
λ / 5,9 | 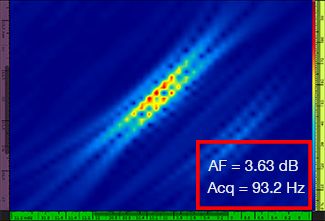 | 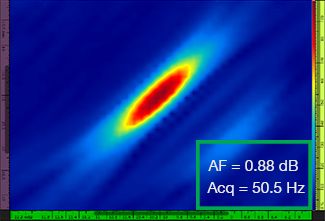 |
λ / 4,0 | 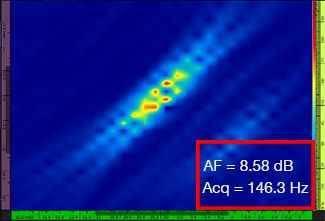 | 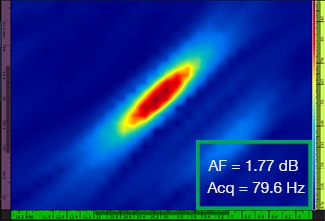 |
Tabulka 1 – Porovnání kvality obrazu mezi standardním snímkem TFM a snímkem s obálkou TFM při čtyřech hodnotách rozlišení rastru. Zobrazené snímky TFM byly přiblíženy. V jednotlivých obrázcích znamená hodnota AF stálost amplitudy, zatímco hodnota Acq odpovídá rychlosti pořizování záznamu, které bylo dosahováno při určitém rozlišení rastru. Červené rámečky označují stav, kdy se nepodařilo dosáhnout hodnoty stálosti amplitudy 2 dB, která je ve shodě s požadavky předpisů a norem. Povšimněte si vyšší rychlosti pořizování záznamu při ekvivalentní hodnotě AF.
Nově vydané předpisy a normy [1, 2] požadují, aby stálost amplitudy činila 2 dB nebo méně. Při použití standardní metody TFM jsou proto ve shodě s těmito předpisy a normami pouze první dvě hodnoty rozlišení rastru (λ / 9,3, λ / 8,1). Obálkou TFM však umožňuje použití hrubšího rozlišení rastru (λ / 4,0) při zachování stálosti amplitudy, která je ve shodě s předpisy a normami. Použití obálky TFM s hrubším rastrem pak umožňuje zvýšení rychlosti pořizování záznamu o přibližně 37 % oproti nejvyšší rychlosti pořizování záznamu, která je dosažitelná za použití standardní metody TFM splňující požadavky předpisů a norem (57,9 Hz při λ / 8,1).
Závěry
Metoda spočívající v provádění výpočtu obálky snímku TFM byla představena a znázorněna za použití jednoduchých příkladů. Názorně jsme předvedli, že obálka signálu je nezávislá na jeho okamžité fázi, a proto poskytuje spolehlivější základ pro postupy amplitudového měření velikostí (jako například pro metodu využívající o pokles o 6 dB). Obálka signálu neslouží pouze k vyhlazování obrazu, a neměla by tedy být považována za filtr, který může způsobovat vznik ztrát dat. Výhody používání obálky při zobrazování metodou TFM byly předvedeny prostřednictvím porovnání snímků TFM pořízených s obálkou a bez obálky a při rozdílných hodnotách rozlišení rastru. Třebaže je k získání výsledné obálky TFM nutno vypočítávat dva snímky TFM, použitím hrubšího rozlišení rastru lze dosahovat významného snížení náročnosti zpracování při zachování shody zbývajících hodnot s požadavky předpisů a norem. Tohoto je dosaženo díky odolnosti obálky proti kolísání amplitudy. Výsledkem je snímek, který je lépe uzpůsoben amplitudovému určování velikosti, přestože je získáván vyšší rychlostí než ekvivalentní snímek zpracovávaný za použití standardní metody TFM.
Použitá literatura
[1] ASME Committee, „ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture“. ASME, 2019.
[2] ASME Committee, „ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matric Capture.“ ASME, 2019.
[3] N. Badeau, A. Le Duff a C.-H. Kwan, „Theoretical Model for Amplitude Fidelity Reading (submitted)“, přednáška na sympoziu ASNT Research Symposium, 2020.
[4] A. C. Clay, S.-C. Wooh, L. Azar a J.-Y. Wang, „Experimental Study of Phased Array Beam Steering Characteristics“, Journal of Nondestructive Evaluation, sv. 18, č. 2, str. 13, 1999.
[5] L. J. Bond, „Fundamentals of Ultrasonic Inspection“, ASM Handbook, sv. 17, č. Nondestructive Evaluation of Material, str. 155–168, 2018.
[6] S.-J. Song, H. J. Shin a Y. H. Jang, „Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components“, Nuclear Engineering and Design, sv. 214, č. 1–2, str. 151–161, květen 2002, datum vydání: 10.1016/S0029-5493(02)00024-9.
[7] S. Mahaut, O. Roy, C. Beroni a B. Rotter, „Development of phased array techniques to improve characterization of defect located in a component of complex geometry“, Ultrasonics, sv. 40, č. 1–8, str. 165–169, květen 2002, datum vydání: 10.1016/S0041-624X(02)00131-2.
[8] S. C. Mondal, P. D. Wilcox a B. W. Drinkwater, „Design of Two-Dimensional Ultrasonic Phased Array Transducers“, Journal of Pressure Vessel Technology, sv. 127, č. 3, str. 336–344, srpen 2005, datum vydání: 10.1115/1.1991873.
[9] S.-C. Wooh a Y. Shi, „Influence of phased array element size on beam steering behavior“, Ultrasonics, sv. 36, č. 6, str. 737–749, duben 1998, datum vydání: 10.1016/S0041-624X(97)00164-9.
[10] Joon-Hyun Lee a Sang-Woo Choi, „A parametric study of ultrasonic beam profiles for a linear phased array transducer“, IEEE Trans. Ultrason., Ferroelect., Freq. Contr., sv. 47, č. 3, str. 644–650, květen 2000, datum vydání: 10.1109/58.842052.
[11] R. Ahmad, T. Kundu a D. Placko, „Modeling of phased array transducers“, The Journal of the Acoustical Society of America, sv. 117, č. 4, str. 1762–1776, duben 2005, datum vydání: 10.1121/1.1835506.
[12] B. W. Drinkwater a P. D. Wilcox, „Ultrasonic arrays for non-destructive evaluation: A review“, NDT & E International, sv. 39, č. 7, str. 525–541, říjen 2006, datum vydání: 10.1016/j.ndteint.2006.03.006.
[13] P. D. Wilcox, „Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing“, v AIP Conference Proceedings, Brunswick, Maine (USA), 2006, sv. 820, str. 845–852, datum vydání: 10.1063/1.2184614.
[14] J. Zhang, B. W. Drinkwater a P. D. Wilcox, „Effects of array transducer inconsistencies on total focusing method imaging performance“, NDT & E International, sv. 44, č. 4, str. 361–368, červenec 2011, datum vydání: 10.1016/j.ndteint.2011.03.001.
[15] C. Holmes, B. W. Drinkwater a P. D. Wilcox, „Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation“, Ultrasonics, sv. 48, č. 6–7, str. 636–642, listopad 2008, datum vydání: 10.1016/j.ultras.2008.07.019.
[16] C. Holmes, B. W. Drinkwater a P. D. Wilcox, „Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation“, NDT & E International, sv. 38, č. 8, str. 701–711, prosinec 2005, datum vydání: 10.1016/j.ndteint.2005.04.002.
[17] D. Gabor, „Theory of Communication“, Journal of the Institution of Electrical Engineers, sv. 96, str. 429–441, 1946.