Phase Coherence Imaging für die Fehlererkennung

1. Einführung

Im Bereich der zerstörungsfreien Prüfung (ZfP) mit Ultraschall ist die Total Focusing Method (TFM) inzwischen ein bekanntes und anerkanntes Bildverarbeitungsverfahren. Zudem ist das Verfahren jetzt in mehrere portable Geräte integriert, die im Handel erhältlich sind, wie in die OmniScan Prüfgeräte der X3-Serie. TFM wird im ZfP-Bereich immer beliebter.

Auch wenn TFM eine einfachere Bildinterpretation als die herkömmliche Phased-Array-Prüfung (PA) ermöglicht, kann die Verwendung eines einzigen Elements bei der Übertragung während der Erfassung zu Bildern mit einem geringen Signal-Rausch-Verhältnis führen. Dieses geringe Signal-Rausch-Verhältnis ist auf eine schlechte akustische Durchdringung zurückzuführen, typischerweise bei dicken Prüfteilen oder stark schallschwächenden Materialien.

Um dieses Problem zu lösen, wird hier eine andere Anwendung des herkömmlichen TFM-Algorithmus vorgeschlagen, nämlich, dass nur die phasenbezogenen Informationen der erfassten Signale verwendet werden. Das Verfahren basiert auf dem Vektorkohärenzfaktor (VCF)¹, der selbst als ein Bild verwendet wird und die Amplitudeninformationen aus den erfassten Signalen entfernt. Dieses Verfahren, allgemein auch als Phase Coherence Imaging (PCI) bekannt, bietet verschiedene Vorteile,^2,3,4, wie:

• Es wird nur die unmittelbare Phase des Signals berücksichtigt². Da die Schallschwächung im Material keinen Einfluss auf die Phase des Signals hat, könnte PCI beim Bewältigen der Herausforderungen bei der Prüfung dicker oder stark schallschwächender Materialien besonders hilfreich sein.
• Da die Amplitude des Signals unberücksichtigt bleibt, entfällt die Notwendigkeit einer Amplitudenjustierung.³
• Verbesserte Empfindlichkeit gegenüber gekrümmten Geometrien und Einheitlichkeit bei der Fehlerdarstellung in den verschiedenen Bildanzeigen.
• Zuverlässige, nicht amplitudenbasierte Methode zur Größenbestimmung von rissartigen Fehlern.³

Im restlichen Dokument werden die Grundprinzipien der PCI-Technologie von Evident erläutert, die teilweise zum Patent angemeldet ist, insbesondere die Methode zur Erzeugung binarisierter Darstellungen von akustischen Echosignalen. Hierzu wird zunächst die Funktionsweise des DAS-Algorithmus (Delay and Sum Algorithm) betrachtet, der es ermöglicht, ein herkömmliches TFM-Bild mit einer Einhüllenden mittels FMC zu erstellen. Anschließend wird demonstriert, dass der PCI-Algorithmus eine Variante des DAS-Algorithmus ist.

Versuchsbeispiele mit hinzugefügten Fehlern bekannter Art und Geometrie ermöglichen den Vergleich von TFM- und PCI-Bildern, die unter Verwendung der PCI- und DAS-Algorithmen ⁵ erhalten werden.

2. Überprüfung der Grundprinzipien der herkömmlichen TFM und des DAS-Algorithmus

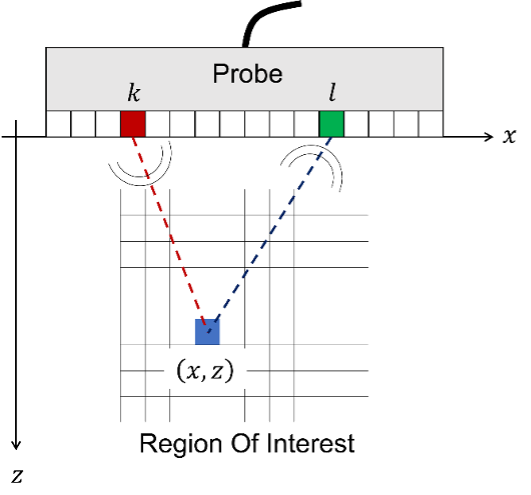
Abbildung 1: Geometrische Konfiguration der FMC-Erfassung mit einem Sensor in Kontakt mit der Prüfteiloberfläche. Das piezoelektrische Element k sendet eine Schallwelle in das Material. Das piezoelektrische Element 1 empfängt die reflektierte Schallwelle.

Abbildung 1 zeigt die FMC-Konfiguration (Full Matrix Capture) eines Phased-Array-Ultraschallsensors (PAUT) und den Prüfbereich, der dem Sensorbereich entspricht, der mit TFM untersucht und betrachtet werden soll. Das piezoelektrische Elementk sendet eine Schallwelle. Diese Schallwelle breitet sich dann im Material des Prüfteils aus und wird von möglichen Fehlern im Material sowie von den verschiedenen Grenzflächen reflektiert. Das piezoelektrische Element l empfängt die reflektierte Schallwelle, die zur Bildung des A-Bild-Signals führt. s_kl . Mittels FMC werden dann alle A-Bilder nach allen möglichen kl Kombinationen geordnet.

Abbildung 2 zeigt ein Flussdiagramm, dass das Prinzip der Rekonstruktion eines herkömmlichen TFM-Bildes durch FMC-Erfassung mittels Verzögerungs- und DAS-Algorithmus in 6 Hauptschritten veranschaulicht:

1. Die FMC-Erfassung erzeugt alle Daten, die aus allen s_kl^I (t) der A-Bilder bestehen. Exponent I gibt dabei an, dass es sich in diesen A-Bildern um Signale in der Phase handelt.
2. Es wird die Hilbert-Transformation angewendet, die es ermöglicht, die Quadraturkomponenten s _kl^Q (t) der A-Bilder in der Phase s_kl^I (t) zu erhalten, die in den FMC-Daten erfasst und gruppiert wurden.
3. Die Daten x_kl^I und x_kl^Q werden unter Verwendung der im Voraus berechneten Verzögerungen τ_kl (x,z) extrahiert. Diese Verzögerungen wurden entsprechend dem ausgewählten Modus (wie LL, TT, TT-T oder TT-TT) und dem Prüfbereich im Voraus berechnet.
4. Die Summierung ergibt dann zwei TFM-Quadraturbilder, I_TFM^I (x,z) und I_TFM^Q (x,z).
5. Die Amplitude (auch Modul oder Hüllkurve genannt) I_TFM (x,z) wird anhand der Formel des euklidischen Abstands geschätzt.
6. In einem Nachbearbeitungsschritt, aktiviert durch die Grafikkarte, wird dann das TFM-Bild formatiert (hauptsächlich durch digitales Filtern, Resampling und Größenanpassung), das dem Benutzer auf dem Gerätebildschirm angezeigt wird.

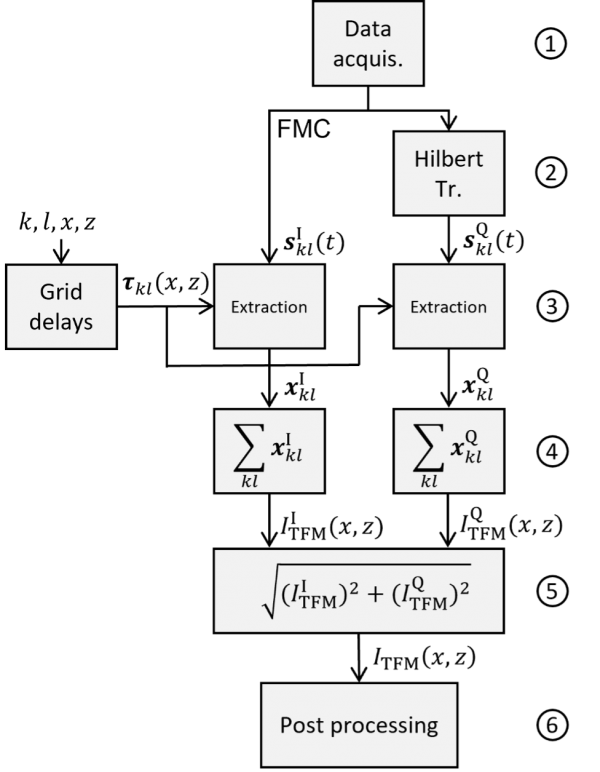
Abbildung 2: Prinzip des DAS-Algorithmus in 6 Schritten zur Erzeugung eines Amplituden-TFM-Bildes aus einer FMC-Erfassung.

3. Prinzipien des PCI-Algorithmus

Der implementierte PCI-Algorithmus des OmniScan X3 64 unterscheidet sich von der herkömmlichen TFM und anderen phasenbasierten Signalverarbeitungstechnologien vor allem dadurch, dass er eine innovative akustische Signalbinarisierungskomponente enthält (zum Patent angemeldet). Der PCI-Algorithmus verglichen mit den in Abbildung 2 dargestellten Schritten des DAS-Algorithmus unterscheidet sich in zwei wesentlichen Punkten:

• Er enthält einen zusätzlichen Schritt 3b (Abbildung 4), der die Signale s _kl^I (t) und s_kl^Q (t) mit der Vorzeichenfunktion quantifiziert. Dieser Schritt ermöglicht, die Kohärenz der Signale hervorzuheben, wie später in diesem Whitepaper erläutert wird.
• Berechnung der Amplitude anhand der Norm L_∞, auch Maximumsnorm genannt, anstelle der Euklidischen Norm, die für die herkömmliche TFM verwendet wird.

3.1. Konzept von PCI

Um den PCI-Algorithmus gut zu verstehen, muss der Begriff der Signalkohärenz eingeführt werden, ein Grundprinzip dieser Methode. Dieser Abschnitt erläutert das Konzept in vereinfachter Form. Dazu muss die Vorzeichenfunktion, auch Signumfunktion genannt, berücksichtigt werden.

Die Vorzeichenfunktion quantifiziert ein Signal s(t) auf 3 verschiedenen Ebenen: 1, 0 und -1.

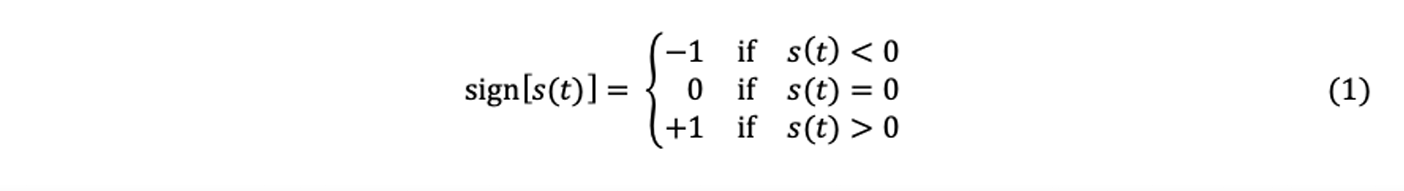
Zum besseren Verständnis der Auswirkungen dieser Quantifizierungsoperation auf die Signale zeigt Abbildung 3 das Ergebnis der angewendeten Vorzeichenfunktion auf ein A-Bild s(t), das hier zu Demonstrationszwecken willkürlich gewählt wurde. Bei Betrachtung von Abbildung 3 ist Folgendes festzustellen:

• Das Signal hat zwei Bereiche: (1) sogenannte kohärente Bereiche, die vorhandene Indikationen anzeigen, die für mögliche Fehler charakteristisch sind; (2) sogenannte nicht kohärente Bereiche, die keine Indikationen, aber vorhandenes Rauschen anzeigen. Es ist zu beachten, dass dieses Rauschen hauptsächlich auf das elektronische Eigenrauschen der Prüfgeräte zurückzuführen ist, aber auch auf strukturelles Rauschen, das durch die Schallwellen im Prüfmaterial entsteht.
• In den kohärenten Bereichen bleibt die Intensität des Signals konstant und liegt zwischen 1 und –1 im quantisierten Signal (Abbildung 3(b)), während die Amplitude im Fall des Rohsignals mit der Zeit abnimmt (Abbildung 3(a)) (z. B. wegen geometriebedingter Schalldämpfung).
• In dem quantisierten Signal in Abbildung 3(b) ist starkes Rauschen mit einem unübersichtlichen Aspekt und einem deutlich höheren Pegel als der fast nicht erkennbare Rauschpegel in dem Rohsignal in Abbildung 3(a) vorhanden. Obiges und die in diesem Dokument folgenden Beispiele zeigen, warum die mit PCI erhaltenen TFM-Bilder "verrauschter" aussehen als herkömmliche TFM-Bilder, wie in Abbildung 6(a) und 6(b) und in Abbildung 8(a) und 8(b) zu sehen ist. Die Bereiche mit einem hohen unübersichtlichen Rauschanteil (nicht kohärente Bereiche) weisen jedoch im Gegensatz zu den kohärenten Bereichen eine von der Position im Bild unabhängige statistische Verteilung auf. Aufgrund dieses Unterschieds und trotz eines verrauschteren Bildes ist es in einem durch PCI erzeugten Bild einfacher, die kohärenten Bereiche von den nicht kohärenten zu unterscheiden. Die anpassbare Farbdarstellung, die standardmäßig im OmniScan X3 64 unter Verwendung von PCI angewendet wird, erleichtert dem Bediener diese Unterscheidung (siehe Abbildung 6(c) und Abbildung 8(c)).

Das Verhalten der Vorzeichenfunktion wird daher von PCI genutzt⁵, um einerseits eine einheitlich Signalintensität (z. B. unabhängig von der Untersuchungstiefe) aufrechtzuerhalten, und andererseits, um die kohärenten Bereiche, die vorhandenen Fehlern entsprechen, von den nicht kohärenten unübersichtlichen Bereichen, die nicht vorhandenen Fehlern entsprechen, zu trennen. Es ist zu beachten, dass die Kohärenz der Signale eine Information ist, die von der Phase des Signals stammt.

Aus einer bestimmten Perspektive kann die von PCI ermittelte Information als binär betrachtet werden, denn Kohärenz/Inkohärenz entspricht vorhandenen/nicht vorhandenen Fehlern. Das Problem besteht also darin, eine Strategie zu wählen, die diese beiden Bereiche voneinander trennt. Die Methode, wie dies erreicht werden kann, wird in diesem Whitepaper nicht behandelt, aber eine anpassbare Farbdarstellung, wie die des OmniScan X3 64 Prüfgeräts, unterstützt eine Unterscheidung.

Abbildung 3: Signal und Rauschen des A-Rohbilds (a) und ein quantisiertes Signal unter Verwendung des Funktionszeichens (b).

3.2. PCI-Algorithmus

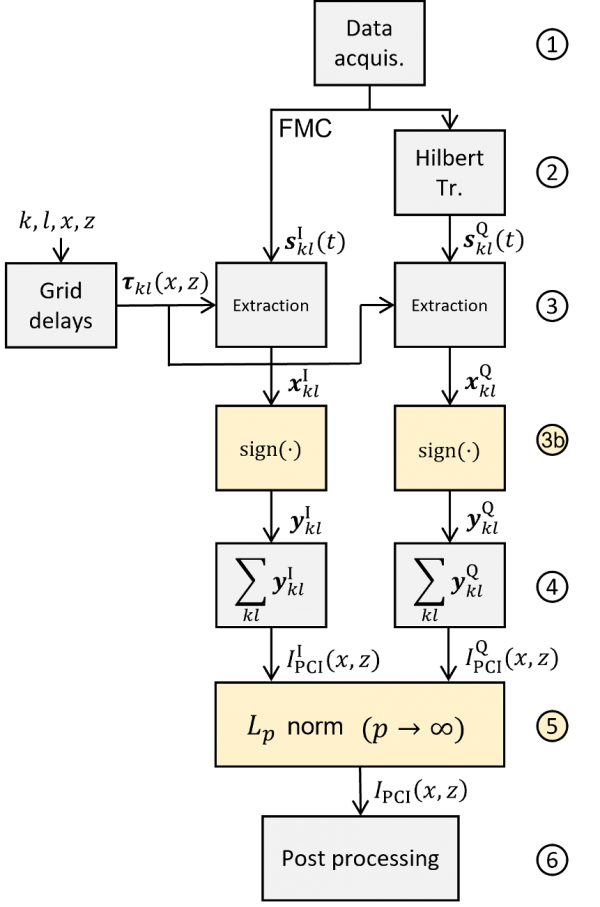
Abbildung 4: Prinzip des PCI-Algorithmus.

Das Flussdiagramm in Abbildung 4 fasst den PCI-Algorithmus des OmniScan X3 64 Prüfgeräts wie folgt zusammen:

1. Erfassungsphase, in der die FMC-Daten erfasst werden, aus denen alle s_kl^I (t) der A-Bilder bestehen. Der Exponent I zeigt an, dass diese A-Bilder Signale in der Phase sind.
2. Anwendung der Hilbert-Transformation, die es ermöglicht, die Komponenten in Quadratur s _Kl^Q (t) der A-Bilder in der Phase s_kl^I (t) zu erhalten, die in den FMC-Daten erfasst und gruppiert wurden.
3. Extraktion der Daten x_kl^I und x_kl^Q unter Verwendung der Verzögerungen τ_kl (x,z). Diese Verzögerungen wurden entsprechend dem ausgewählten Modus (wie L-L, T-T, TT-T, TT-TT) und dem Prüfbereich im Voraus berechnet.

Diese ersten drei Schritte sind identisch mit denen des DAS-Algorithmus in Abbildung 2.

3b. Quantisierung der Signale x_kl^I und x_kl^Q unter Verwendung der Vorzeichenfunktion nach Formel 1, was zu Signalen y _kl^I und y_kl^Q führt:

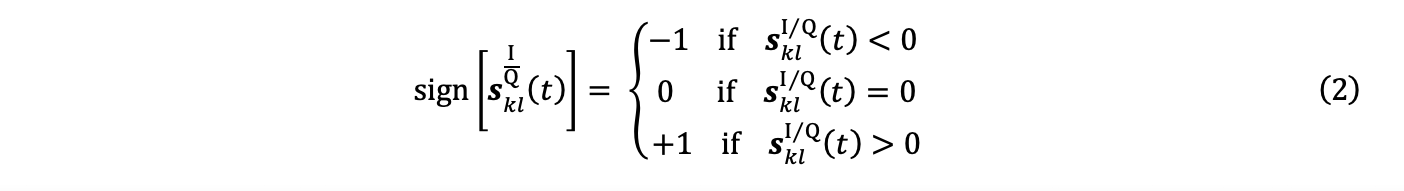
Schritt 3b ist ein zusätzlicher Schritt, der spezifisch für den PCI-Algorithmus ist.

4. Die Summierung ergibt zwei PCI-Quadraturbilder, I_PCI^I (x,z) und I_PCI^Q (x,z):

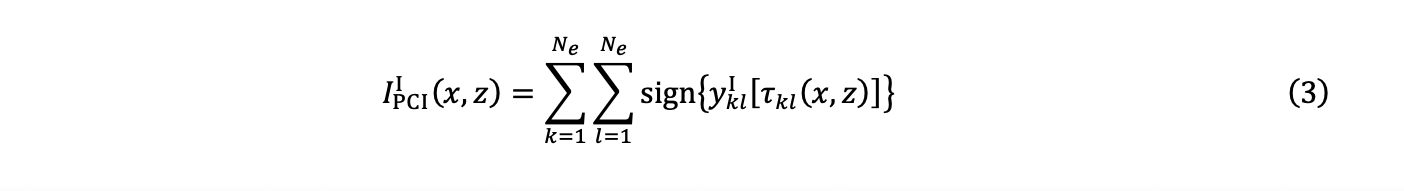
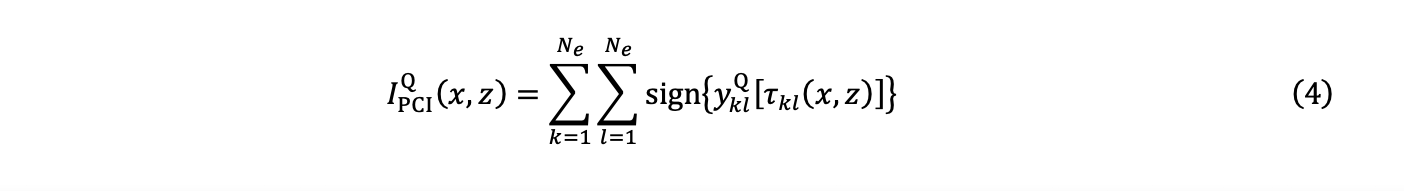
5. Schließlich wird die Amplitude I_PCI (x,z) mit der Berechnung nach der Maximumsnorm oder der Norm L_∞ und der beiden Komponenten der Gleichungen (3) und (4) geschätzt:

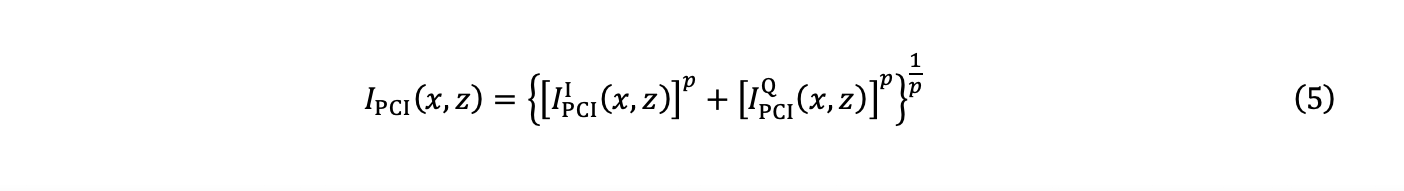
mit p→∞.

Die Ermittlung der Amplitude durch Formel 5 ist mit p→∞ schwierig zu erreichen. Eine gute Annäherung erhält man nach folgender Formel:

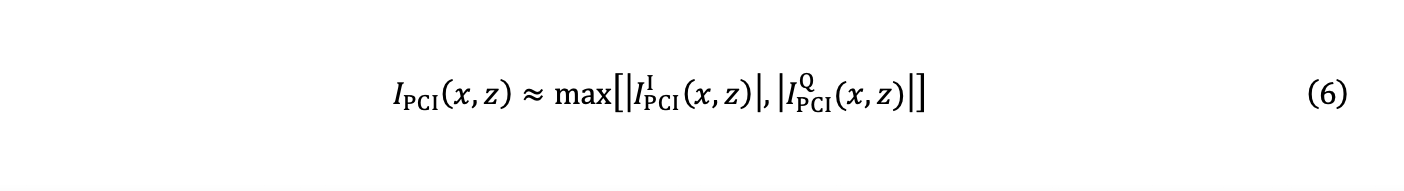
Das heißt, der Endwert ist das Maximum der Absolutwerte (|⋅|) in der Phase und der Quadraturbilder.

6. Der abschließende Nachbearbeitungsschritt ist mit dem DAS-Algorithmus identisch. Er wird verwendet, um ein herkömmliches TFM-Bild durch die Grafikkarte zu erhalten, die das TFM-Bild formatiert (hauptsächlich digitales Filtern, Resampling und Größenanpassung), das dem Benutzer auf dem Gerätebildschirm angezeigt wird.

Es ist zu erwähnen, dass die PCI-Verarbeitung (siehe Abbildung 4) des OmniScan X3 64 Prüfgeräts mit einer Prüfgeschwindigkeit (d. h. von der Datenerfassung bis zur Bildgebung) durchgeführt wird, die etwa der des herkömmlichen TFM-Modus des Geräts entspricht.

4. Versuchsbeispiele

Zwei Beispiele, Auszüge aus Versuchsbeispielen mit Fehlern bekannter Art und Geometrie, werden im Folgenden demonstriert, um Bilder zu vergleichen, die unter Verwendung der beiden zuvor beschriebenen Algorithmen erhalten wurden und um bestimmte Eigenschaften von PCI hervorzuheben. Dazu gehören Amplitudenrobustheit und Rissspitzenempfindlichkeit.

4.1. Beispiel 1: Block mit Querbohrungen

Das erste Versuchsbeispiel soll die Robustheitseigenschaften der Schalldämpfung des PCI-Verfahrens hervorheben. Ein Stahlblock mit 17 Querbohrungen (ASTM E2491 Block aus kohlenstoffarmem Stahl) wird ohne Vorlaufkeil (d. h. Sensor berührt das Prüfteil) unter Verwendung eines 5L64-A32 PAUT-Sensors geprüft. Diese Prüfkonfiguration ist in Abbildung 5 dargestellt.

Abbildung 6 zeigt ein rekonstruiertes herkömmliches TFM-Bild (a) und PCI-Bilder (b und c) unter Verwendung des L-L-Ausbreitungsmodus. In Abbildung 6 ist Folgendes deutlich zu erkennen:

• Alle Querbohrungen werden im PCI-Bild mit der gleichen Intensität angezeigt, wohingegen im herkömmlichen TFM-Bild der Effekt der Schalldämpfung an den unteren Querbohrungen und der Effekt der Amplitude der Schallbündel an den oberen Querbohrungen sichtbar ist.
• Auch das Hintergrundrauschen ist im PCI-Bild höher.

Da es sich bei PCI um ein amplitudenfreies Bildgebungsverfahren handelt, erfolgt die kohärente Summierung von Signalen unabhängig von der Amplitude der Signale und erzeugt somit Anzeigen mit hohem Kontrast.³

Abbildung 5: Prüfkonfiguration – Beispiel 1: ASTM E2491 Block aus kohlenstoffarmem Stahl und 5L64-A32 Sensor.

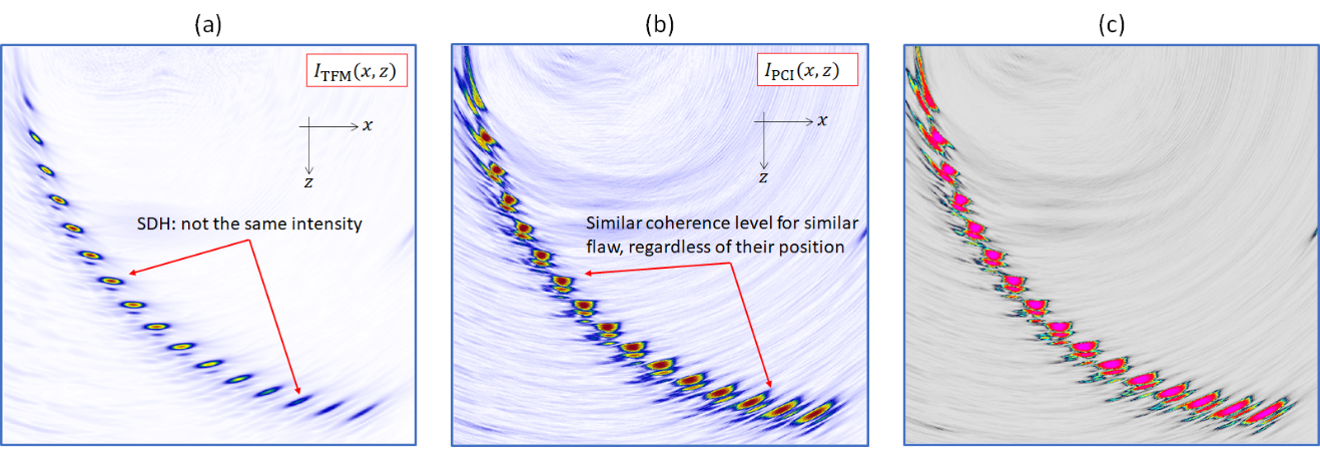
Abbildung 6: Bildgebung der Querbohrungen mit herkömmlichem TFM (a), PCI (b) und PCI mit der Standardfarbdarstellung des OmniScan X3 64 Prüfgeräts.

4.2. Beispiel 2: Block mit Kerbe

Eine weitere interessante Eigenschaft von PCI ist die Empfindlichkeit gegenüber Rissspitzen, die eine genaue Größenbestimmung von Diskontinuitäten ermöglicht. Anscheinend werden Spiegelreflexionen von großen Streuungen in Bezug auf die Amplitudensummierung reduziert, da nur wenige gemeinsame Phasenbedingungen zur Summierung beitragen. Daher ist PCI tendenziell stabiler für schmale und spitze Reflektoren.

Um diese Eigenschaft von PCI hervorzuheben, zeigt das zweite Beispiel die Prüfergebnisse eines Stahlblocks, der eine nicht oberflächenbrechende Kerbe im 70°-Winkel enthält, unter Verwendung eines SPWZ1-N55S-IHC Vorlaufkeils und eines 7.5L60-PWZ1 Phased-Array-Sensors. Abbildung 7 zeigt die Prüfkonfiguration.

Abbildung 8 zeigt ein rekonstruiertes herkömmliches TFM-Bild (a) und PCI-Bilder (b und c) unter Verwendung des TT-TT-Ausbreitungsmodus. Folgende Vergleiche sind möglich:

• Spiegelreflexionen von großen Streuungen werden in Bezug auf die Amplitudensummierung reduziert, da nur wenige gemeinsame Phasenbedingungen zur Summierung beitragen.
• Der Kontrast wird für PCI im Vergleich zur herkömmlichen TFM verbessert.
• PCI bietet eine bessere Empfindlichkeit gegenüber Rissspitzen.
• Das Signal-Rausch-Verhältnis ist bei PCI geringer.

Auch wenn in diesem Fall ein herkömmliches TFM-Bild eine genauere Einschätzung der Größe der Kerbe ermöglicht, kann PCI aufgrund der hohen Empfindlichkeit gegenüber Rissspitzen die Größe von kerbartigen Fehlern ohne die Verwendung von halbempirischen Erhebungen, die leicht durch Justierverfahren oder Schalldämpfung im Material fehlerhaft sein können, genau bestimmen.

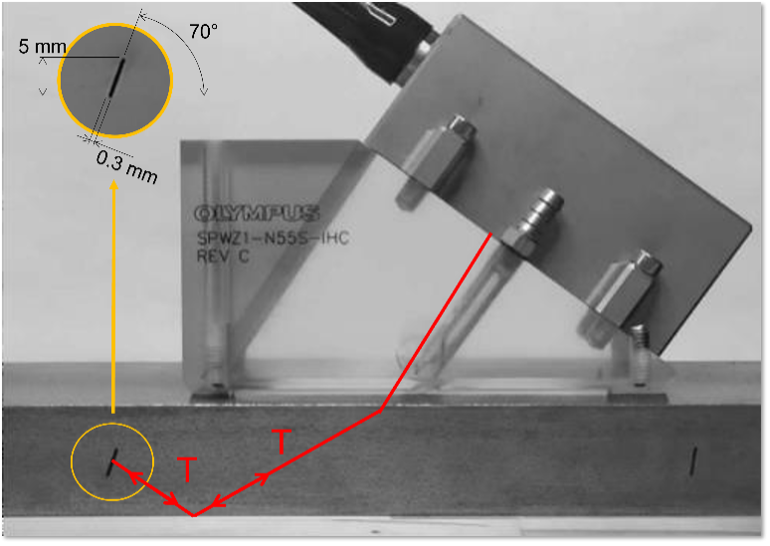
Abbildung 7: Prüfkonfiguration - Beispiel 2: ein kohlenstoffarmer Stahlblock mit einer schrägen Kerbe, hergestellt durch funkenerosives Bearbeiten, unter Verwendung eines SPWZ1-N55S-IHC Vorlaufkeils und eines 7.5L60-PWZ Sensors.

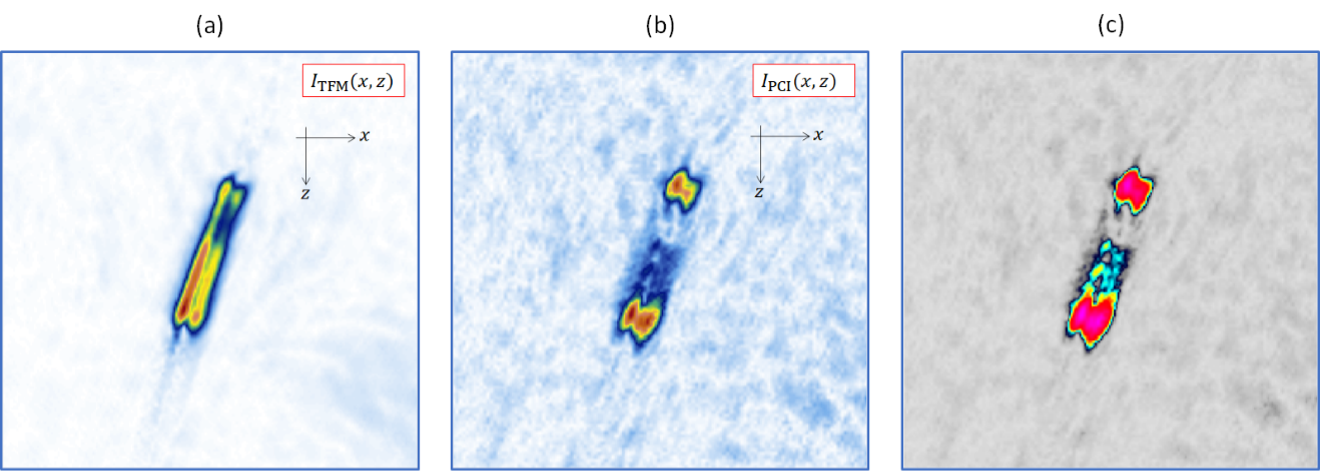
Abbildung 8: Bildgebung der Kerbe mit herkömmlichem TFM (a), PCI (b) und PCI mit der Standardfarbdarstellung des OmniScan X3 64 Prüfgeräts.

Ergebnisse der Versuchsbeispiele

Zusammenfassend haben unsere Prüfkonfigurationen gezeigt, dass PCI viele Vorteile bietet:

• Da es sich um ein nicht amplitudenbasiertes Bildgebungsverfahren handelt, basiert die Bildinterpretation nicht auf amplitudenjustieren Signalen, was ein Vorteil gegenüber der amplitudenbasierten herkömmlichen TFM ist.
• Höhere Empfindlichkeit gegenüber schmalen und spitzen Reflektoren und gegenüber gekrümmten Geometrien.
• Ermöglicht eine genaue Größenbestimmung von kerbartigen Fehlern ohne Verwendung von halbempirischen Erhebungen, die leicht durch Justierverfahren oder Schalldämpfung im Material fehlerhaft sein können.
• Ein Justierverfahren ist nicht erforderlich, wodurch die Größenbestimmung von Kerben im Vergleich zu herkömmlicher TFM einfacher und genauer wird.
• Die Verstärkung kann auf einen sehr niedrigen Wert eingestellt werden, wodurch eine Signalsättigung verhindert wird.
• Zudem erzeugt ein Gerät mit einem ausreichend leistungsstarken Prozessor, wie das OmniScan X3 64 Prüfgerät, Live-PCI-Bilder, sodass die Ergebnisse während der Prüfung sofort angezeigt werden.

Einige Nachteile dieser Methode sollten jedoch auch erwähnt werden:

• Planare Reflektoren werden nur unzureichend reproduziert.
• Das Signal-Rausch-Verhältnis von PCI ist niedriger als bei amplitudenbasierten Methoden. Doch wie bereits erwähnt, ist dies kein großer Nachteil, denn PCI ermöglicht eine einfache Unterscheidung zwischen kohärenten Bereichen, die vorhandene Fehler anzeigen, und inkohärenten Bereichen, die verrauschten Bildbereiche anzeigen.
• Bediener sind daran gewöhnt, amplitudenbasierte Bilder zu sehen, daher kann eine Anpassungsphase erforderlich sein.

Literaturnachweis

1. JF Cruza, J. Camacho und C. Fritsch: Plane-wave phase-coherence imaging for NDE. NDT & E International, Vol. 87, S. 31–37, April 2017.
2. B. Gauthier, G. Painchaud-April, A. Le Duff und P. Belanger: Lightweight and Amplitude-Free Ultrasonic Imaging Using Single-Bit Digitization and Instantaneous Phase Coherence. IEEE Trans. Ultrason., Ferroelektr., Freq. Contr., Vol. 69, Nr. 5, S. 1763–1774, Mai 2022, doi: 10.1109/TUFFC.2022.3163621.
3. B. Gauthier, G. Painchaud-April, A. Le Duff und P. Bélanger: Towards an Alternative to Time of Flight Diffraction Using Instantaneous Phase Coherence Imaging for Characterization of Crack-Like Defects. Sensors, Vol. 21, Nr. 3, S. 730, Jan. 2021, doi: 10.3390/s21030730.
4. A. Le Duff, N. Badeau, E. Peloquin, G. Painchaud-April, C.-H. Kwan, B. Gauthier: „Total Focusing Method with Phase-Only Ultrasound Signal for Small Flaw Detection. International Ultrasonic Testing Conference (UT-Online), 2021.
5. G. Painchaud-April, A. Le Duff, C. Kwan. C. Brillon, Phase-Based Approach for Ultrasonic Inspection, World Intellectual Property Organization (WIPO). 02.09.2021. WO/2021/168565 https://patentscope.wipo.int/search/fr/detail.jsf?docId=WO2021168565=EP383773045