Autores: Nicolas Badeau, Guillaume Painchaud-April y Chi-Hang Kwan
Resumen
La técnica de inspección de método de focalización total (TFM, por sus siglas en inglés) ahora está incluida en los estándares y los códigos que regulan las pruebas no destructivas (NDT), como ASME Sección V. Un parámetro importante especificado en estos códigos para la planificación del barrido de TFM es la fidelidad de amplitud. Se define como la variación en la amplitud obtenida para un reflector específico, debido a la resolución finita de la retícula de imagen. El umbral de fidelidad de amplitud permitido típico en estos códigos es un máximo de 2 dB. Aunque los códigos sugieren los métodos experimentales para medir la fidelidad de amplitud de una configuración específica, en este documento se propone un método analítico sencillo y conservador. El uso de la envolvente de TFM también se considera en la estimación de la fidelidad de amplitud, ya que permite usar una retícula de TFM menos densa sin generar un valor de fidelidad de amplitud que supere la tolerancia definida. Para el procesamiento de imágenes estándar de TFM, los resultados empíricos mostraron que se necesita una resolución de retícula de unos λ0/10 para obtener una fidelidad de amplitud inferior a 2 dB. Para el procesamiento de imágenes de TFM con la envolvente, los resultados empíricos mostraron la necesidad de contar con una resolución de la retícula de λ0/3,3 para cumplir el código.
Introducción
El método de focalización total (TFM) es una nueva técnica aceptada para realizar ensayos no destructivos (NDT) en los componentes. Los estándares y códigos, como ASME V [1], han integrado una captura de matriz completa (FMC) y TFM como una técnica de inspección ultrasónica adicional de phased array. Aunque los métodos FMC/TFM son relativamente nuevos en la industria de NDT, se vienen utilizado durante algún tiempo en aplicaciones médicos como estándar de referencia para el procesamiento de imágenes médicas ultrasónicas [2–4]. De hecho, la mayoría de técnicas de procesamiento de imágenes médicas ultrasónicas suelen referenciarse y compararse con el procesamiento de imágenes de TFM.
Aunque existen técnicas similares a FMC/TFM (p. ej. VTFM [5], IWEX [6], SAFT [7]), el algoritmo utilizado más frecuentemente es el procesamiento de retardo y suma [2–4,8,9]. La técnica de FMC/TFM consiste en un esquema de adquisición (FMC) basado en la adquisición de la señal de todas las combinaciones de elementos del transmisor y el receptor, y un esquema de suma (TFM), que calcula el resultado del haz ultrasónico focalizado en varias ubicaciones de una región de interés. La región de interés de TFM se suele mallar sobre una retícula cartesiana y las intersecciones individuales de la retícula a la que se aplica la focalización acústica se conocen como píxeles. El método de focalización es simular al procesamiento de imágenes ultrasónicas de phased array estándar, excepto en que los haces se forman en el procesamiento posterior usando los datos almacenados en la matriz de datos de FMC. El proceso de retardo y suma posterior a la adquisición asume la linealidad de las ondas acústicas subyacentes encontradas en las aplicaciones típicas de NDT.
La técnica de FMC/TFM puede verse como una extensión natural de la técnica phased array convencional. Sin embargo, deben considerarse nuevos parámetros de configuración debido a las diferencias en la representación de datos en comparación con las pruebas ultrasónicas de phased array convencionales (PAUT). Uno de estos conceptos es la fidelidad de amplitud (AF) de una retícula de TFM. La AF se define como la variación de amplitud máxima de una indicación provocada por una resolución de la retícula de TFM {Δx,Δz}. La utilización de una retícula cartesiana uniforme, p. ej. (Δx=Δz) se considera para el resto de este estudio. La fidelidad de amplitud puede expresarse formalmente como
![(Eq.1) AF(Δx)≡-20 registro〖(A_(máx. muestra) (Δx))/A_(máx. real 〗 [dB]](https://static3.olympus-ims.com/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=17FA)
donde Amáx. muestra es la amplitud máxima medida de un elemento de interés basado en el muestreo de la retícula finita, y Amáx. real es el máximo del mismo elemento de interés basado en una resolución de retícula infinita. El límite al que el tamaño de la retícula es cero en los dos ejes para Amáx. muestra (Δx) define Amáx. real, y la fidelidad de amplitud correspondiente pasa a ser 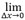 AF(Δx)=0. La ecuación 1 proporciona una definición formal para calcular la fidelidad de amplitud en relación con la resolución de la retícula. En la práctica, con todo, el máximo real Amáx. real de la señal subyacente solo puede estimarse haciendo un muestreo excesivo de la interpolación y la imagen de amplitud de TFM,
AF(Δx)=0. La ecuación 1 proporciona una definición formal para calcular la fidelidad de amplitud en relación con la resolución de la retícula. En la práctica, con todo, el máximo real Amáx. real de la señal subyacente solo puede estimarse haciendo un muestreo excesivo de la interpolación y la imagen de amplitud de TFM,
![(Eq.2) (AF) ̂(Δx)=-20 registro〖(A_(máx. muestra) (Δx))/A ̂_(máx. real) 〗 [dB]](https://static5.olympus-ims.com/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=17FA)
donde 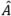 máx. real es una estimación de Amáx. real.
máx. real es una estimación de Amáx. real.
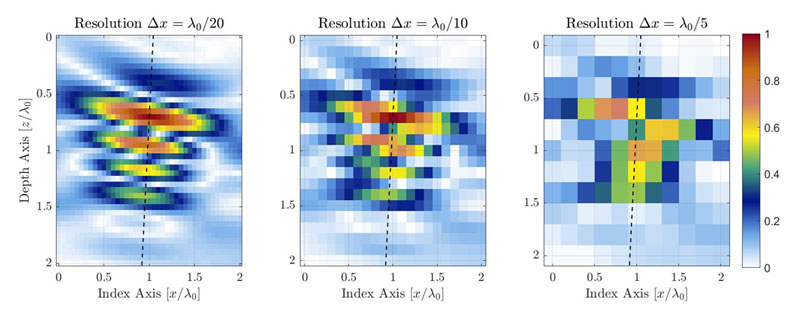
Figura 1. Ilustración de la degradación en la calidad de imagen de TFM provocada por la reducción de la resolución de la retícula de TFM. Las líneas de puntos representan el eje principal de la propagación acústica.
Para una zona de interés idéntica, una resolución mayor de la retícula tendrá un recuento de píxeles inferior. La Figura 1 muestra imágenes de TFM típicas del mismo orificio taladrado lateral (SDH) para los diversos valores de resolución de retícula. La resolución de la retícula se define como una fracción de la longitud de onda de frecuencia central de la sonda λ0= c/f0, donde es la velocidad acústica en la pieza y f0 es la frecuencia central de la sonda.
Los estándares y códigos ahora incluyen un requisito para ajustar la fidelidad de amplitud a un valor máximo de 2 dB [1,10]. Este requisito se deriva del compromiso aplicativo entre una calidad de imagen suficiente para garantizar un análisis apropiado de NDT y la productividad de inspección, que se ve afectada en gran medida por la densidad de la retícula de TFM en una región de interés especificada. Debemos tener en cuenta que el equilibrio entre calidad de imagen de TFM y productividad de inspección es especialmente crítico para los dispositivos portátiles autónomos que no tienen acceso a una gran potencia de procesamiento. Este problema se espera que desaparezca en el tiempo, ya que el hardware incorporado mejora la eficiencia energética y la computación remota está más disponible que antes.
Aunque se han propuesto algunos métodos empíricos [10–12], suelen requerir una computación extensiva y los resultados obtenidos no son representativos de la amplitud real provocada por la resolución de la retícula, que es otro tema que abordaremos en la sección siguiente. Este documento representa un método para estimar con precisión la fidelidad de amplitud de una configuración de TFM para ayudar al técnico de NDT a realizar una inspección de TFM productiva y conforme a las normas.
El documento se divide de la forma siguiente. En primer lugar, se incluye una explicación completa del problema que deben afrontar los técnicos de NDT. Después se describe un método para medir empíricamente la fidelidad de amplitud de una configuración de TFM. En la sección siguiente se propone un modelo analítico para estimar la fidelidad de amplitud. Después el modelo propuesto se compara con las mediciones empíricas en tres casos de uso de TFM diferentes. Después se incluye una breve conclusión explicando el trabajo realizado.
Problemática
Mientras que una retícula muy fina (densa) permite una fidelidad de amplitud muy pequeña, los dispositivos electrónicos contemporáneos capaces de calcular las imágenes de TFM en vivo siguen teniendo límites computacionales. Una resolución más fina de la retícula sobre una región de interés significa que hay una gran cantidad de puntos de enfoque que reducen la productividad de la inspección y la velocidad de barrido mecánico. El técnico de NDT también debe poder seleccionar una resolución adecuada de una retícula que maximice la productividad de inspección y mantenga el cumplimiento normativo.
La fidelidad de amplitud puede ilustrarse con una muestra de señal simple en una dimensión en diversos periodos. En el ejemplo mostrado en la Figura 2, la señal unidimensional mostrada es la amplitud de SDH presentada en la Figura 1 junto con el eje de propagación acústica, extraída de una imagen de λ0/100 en alta resolución. Para mostrar el ejemplo, solo se presenta una sección ampliada cerca de la amplitud máxima de la señal. De nuevo, las mediciones en tres resoluciones diferentes λ0/20, λ0/10 y λ0/5 se identifican por medio de círculos azules sobre una referencia interpolada en alta resolución (curva negra plana).
(a) La resolución de la retícula discreta es λ0/20 y la fidelidad de amplitud calculada es AF = 0,27 dB. |
(b) La resolución de la retícula discreta es λ0/10 y la fidelidad de amplitud calculada es AF = 0,82 dB. |
(c) La resolución de la retícula discreta es λ0/5 y la fidelidad de amplitud calculada es AF = 3,7 dB. |
Figura 2. Ilustración del efecto del periodo de muestreo en la amplitud registrada a lo largo del eje de propagación ilustrado en la Fig. 1. Se muestra una referencia de señal interpolada en alta resolución (línea negra) para facilitar la visualización. La fidelidad de amplitud conforme al código de 2dB se representa por medio de una línea de puntos roja.
La conclusión obvia es que una retícula más densa proporciona una mejor representación de una señal continua, cuantificada por el valor de AF en la Ecuación 1, pero el problema de la optimización sigue existiendo: ¿cuál es el tamaño máximo de la retícula (Δxmáx ) que garantice que todas las posiciones posibles de la retícula sobre una imagen de TFM, una fidelidad de amplitud de 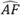 que es igual al valor objetivo de AFobjetivo? O,
que es igual al valor objetivo de AFobjetivo? O,
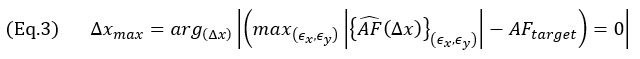
En este planteamiento del problema queda claro que todas las traducciones de la retícula, identificadas por los desplazamientos (ϵx,ϵy), deben tenerse en cuenta para obtener la 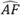 máxima para un tamaño de célula específico (Δx). Esto se hace para cubrir todos los casos posibles de colocaciones de la retícula para calcular la imagen de TFM.
máxima para un tamaño de célula específico (Δx). Esto se hace para cubrir todos los casos posibles de colocaciones de la retícula para calcular la imagen de TFM.
En la sección siguiente, se incluye una ilustración del principio de medición para el conjunto de valores de fidelidad de amplitud producida por varios desplazamientos de la retícula {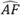 (Δx)}(ϵx,ϵy).
(Δx)}(ϵx,ϵy).
Medición empírica de la fidelidad de amplitud
Antes de explicar cómo podemos estimar la fidelidad de amplitud usando el modelo analítico simple, es de vital importancia definir cómo podemos medirla experimentalmente en el caso de una imagen de TFM. En la industria de NDT se han descrito y propuesto diversas técnicas [10–12], pero algunas de ellas no cuantifican la fidelidad de amplitud completamente. La medición empírica de la fidelidad de amplitud puede pasar a ser rápidamente una carga de adquisición para el técnico de NDT, ya que requiere calcular una gran cantidad de imágenes de TFM desde varias posiciones de la retícula de TFM de forma precisa.
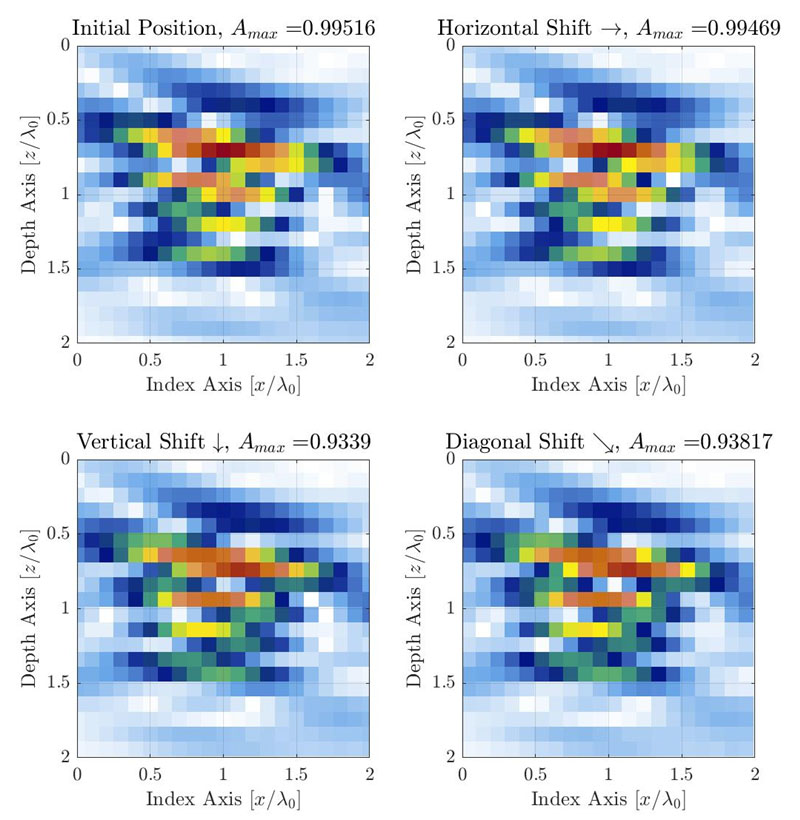
Figura 3. Ilustración de la variación de AF producida por la resolución de la retícula discreta a medida que la retícula se desplaza a 3 posiciones diferentes. La resolución de la retícula se fija en Δx=Δy=λ0/10. La retícula se desplaza una cuarta parte de la celda de la retícula hacia la derecha (ϵx=λ0/40,ϵy=0) (parte superior derecha), parte inferior (ϵx=0,ϵy=λ0/40) (parte inferior izquierda) y diagonalmente (ϵx=λ0/40,ϵy=λ0/40) (parte inferior derecha).
Para aplicaciones de TFM típicas, se utiliza un SDH a modo de defecto de referencia para calibrar la amplitud y medir la fidelidad de amplitud [1,10]. La amplitud observada variará en mayor medida en el eje principal de la propagación acústica, que es una función de la posición de la sonda, la suela (zapata) y el objetivo en la región de interés (p. ej. la posición de la retícula TFM respecto de la sonda). En el caso ilustrado en la Figura 1, el eje principal de propagación es casi vertical. Sin embargo, para un método de medición genérico, el eje de propagación será diferente dependiendo de la ubicación dentro de la región de interés. Para una imagen de TFM, la retícula de muestreo debe moverse en todas las direcciones para capturar la verdadera variación de amplitud provocada por la retícula discreta. Este proceso se ilustra más abajo con el mismo ejemplo de la Figura 1 (centro), que tiene una resolución de la retícula de λ0/10.
Se sugiere mover la retícula una fracción de la resolución de la retícula que va a probarse (p. ej. una vigésima parte de la resolución) en todas las direcciones las veces que sea necesario para superponer la retícula. Esto significa que, para poder cubrir una compensación de la resolución de una retícula en las dos direcciones ortogonales, es necesario realizar un total de 202 = 400 pasos de desplazamiento (si se usa el paso de retícula sugerido de una vigésima parte de la resolución). La amplitud máxima se registra para cada compensación de la retícula, y los valores máximo y mínimo registrados se utilizan para obtener la fidelidad de amplitud usando la Ecuación 2. En el caso presentado en la Figura 3, la resolución de la retícula es λ0/10 y la fidelidad de amplitud medida es 0,88 dB. Si observamos el número de desplazamientos necesarios, podemos anticipar que este proceso manual será tedioso y laborioso para el técnico de NDT. Esto también significa que es necesario calcular un total de 400 imágenes de TFM para medir la fidelidad de amplitud de una resolución de retícula individual.
Cabe mencionar que usando el desplazamiento del software de la posición de la retícula de TFM relativa a la sonda insertada de un desplazamiento mecánico de la sonda relativo a la parte como se propone en ASME Sección V [12], es posible generar múltiples imágenes de TFM usando un único conjunto de datos de FMC. La otra ventaja de este enfoque es la capacidad de acceder al componente vertical de la retícula. De hecho, la sonda y la suela (zapata) no pueden moverse mecánicamente en relación con el SDH seleccionado en el eje de profundidad.
Algunos dispositivos de NDT proporcionan fácilmente herramientas semiautomatizadas que desplazan la retícula de TFM, registran la amplitud máxima en la región de interés y calculan la fidelidad de amplitud resultante en última instancia [11]. Sin embargo, estas herramientas normalmente solo desplazan la retícula en dirección horizontal y, en consecuencia, realizan una estimación insuficiente de la fidelidad de amplitud. A modo comparativo, si la retícula se mueve solo por el eje horizontal, por ejemplo, cómo podemos ver en la Figura 3, la fidelidad de amplitud medida es de 0,06 dB, que es más de 15 veces inferior a la fidelidad de amplitud medida si se considera el eje vertical.
Modelo fenomenológico para estimar la fidelidad de amplitud
Esta sección propone un modelo analítico simple basado en la observación empírica. El modelo fenomenológico considera el comportamiento de la señal en el eje principal de propagación, que se asume que contiene la mayoría de las fluctuaciones de amplitud y, por lo tanto, es más sensible a la resolución de la retícula. La Figura 4 muestra el perfil empírico de una imagen de TFM resultante de un SDH en el eje principal de propagación (azul) y en el eje de concentración del haz (rojo). El origen del eje está situado en la ubicación de amplitud máxima aparente de la representación de la envolvente, que explica la pequeña compensación en el eje 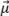 para la representación oscilatoria. Se proporcionan los perfiles para el TFM oscilatorio estándar y para la envolvente del TFM.
para la representación oscilatoria. Se proporcionan los perfiles para el TFM oscilatorio estándar y para la envolvente del TFM.
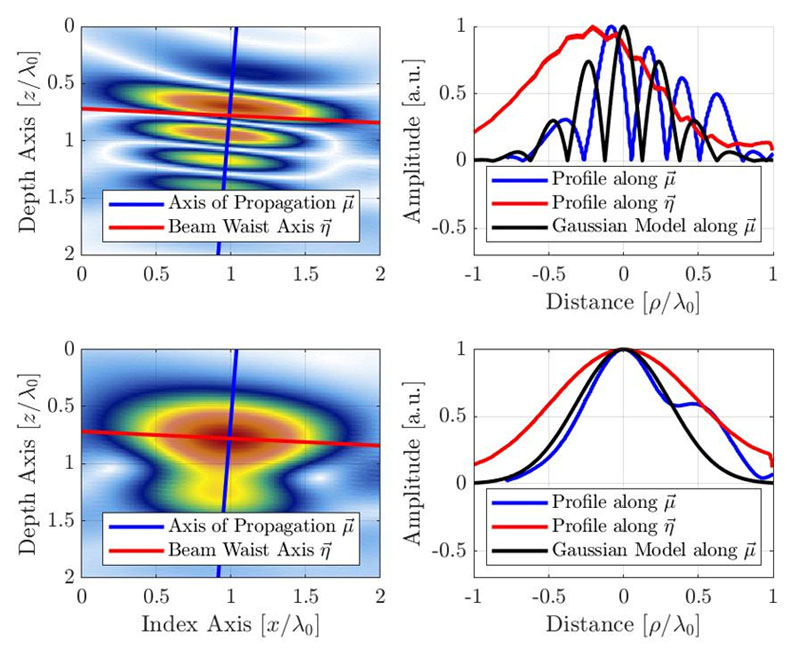
Figura 4. Imagen de TFM (parte superior: oscilatoria, inferior: envolvente) con el perfil de señal en el eje de propagación acústica y el eje de concentración del haz. El modelo gaussiano propuesto también se ilustra para las imágenes de TFM oscilatoria y de envolvente. Podemos observar que la longitud de onda aparente se ha reducido a la mitad debido a la naturaleza de emisión-recepción de la formación el haz de TFM.
Como hemos dicho anteriormente, se asume que el eje con la mayor variación de amplitud es el eje principal de la propagación acústica. De ahí que el modelo pretende reproducir la variación de la amplitud en esta dirección. La señal del modelo es un modelo gaussiano con modulación de coseno
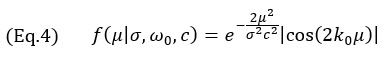
donde k0=ω0/c es el número de onda en la frecuencia angular central ω0 de la sonda, σ es el parámetro de ancho que depende de la frecuencia central y el ancho de banda relativo bw. El parámetro de ancho σ se calcula usando
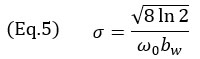
Para una sonda de NDT phased array típica, el ancho de banda relativo está cerca de la marca del 60%, por lo que se utiliza un valor de (bw=0,6) en el modelo. Esto, a su vez, hace que la envolvente gaussiana sea más grande que una oscilación única del coseno. Cabe mencionar que la frecuencia central del término coseno en la Ecuación 3 es el doble de la frecuencia central de la sonda. Esto se debe a la naturaleza de emisión-recepción del procesamiento de imágenes de TFM (trayectoria de transmisión y recepción) y puede observarse en la distancia existente entre las oscilaciones en la Figura 4. De hecho, la conversión entre el dominio de tiempo y el dominio de espacio se escribe como μ = tc/2. Esto también explica el factor 2 usado como el término exponencial de la Ecuación 3.
Para el modelo oscilatorio de la Ecuación 4, dado que la envolvente gaussiana es mucho más grande que una única oscilación de la función de coseno, solo se consideran los valores |μ|≤λ0/8, ya que los valores más grandes producirían un solapamiento espacial para la AF.
Para el modelo de la envolvente de TFM, solo se utiliza el término gaussiano de la Ecuación 4 que da el siguiente resultado
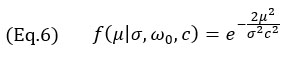
que es válido para cualquier resolución de retícula. El perfil objetivo con el modelo de las Ecuaciones 3 y 7 se ilustra en la Figura 5 en los perfiles experimentales. Tenga en cuenta que las mediciones empíricas también muestran la señal de onda de superficie (el eco envolvente típico de los SDH) retardado detrás del eco principal, una característica que está ausente en el modelo propuesto.
La orientación del defecto respecto de los ejes ortogonales de la retícula debe considerarse para poder obtener la fidelidad de amplitud en el escenario de peor caso con el modelo. Como podemos ver en la Figura 5a, el escenario de peor caso para la TFM oscilatoria ocurre cuando el eje principal de la propagación acústica 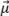 es paralelo a uno de los ejes de la retícula. Por ello, la fidelidad de amplitud debe calcularse como si la amplitud máxima estuviera centrada entre dos puntos de la retícula en cualquiera de los ejes
es paralelo a uno de los ejes de la retícula. Por ello, la fidelidad de amplitud debe calcularse como si la amplitud máxima estuviera centrada entre dos puntos de la retícula en cualquiera de los ejes 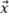 o
o 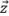 , dando como resultado
, dando como resultado
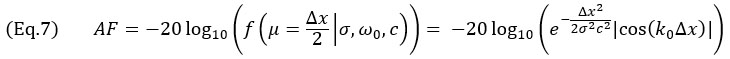
para Δx≤λ0/4. Para la envolvente de TFM, el escenario de peor caso ocurre cuando el perfil de amplitud es idéntico en el eje principal de propagación 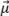 y el eje de concentración del haz
y el eje de concentración del haz 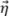 . Este caso, ilustrado en la Figura 5b, corresponde a la representación de SDH como un círculo y, por ello, el eje principal de propagación
. Este caso, ilustrado en la Figura 5b, corresponde a la representación de SDH como un círculo y, por ello, el eje principal de propagación 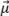 puede tener cualquier orientación. El escenario de peor caso ocurre cuando el eco de SDH se centra entre cuatro puntos adyacentes, como se muestra. En este caso, la fidelidad de amplitud debe calcularse en la diagonal de la retícula, dando como resultado
puede tener cualquier orientación. El escenario de peor caso ocurre cuando el eco de SDH se centra entre cuatro puntos adyacentes, como se muestra. En este caso, la fidelidad de amplitud debe calcularse en la diagonal de la retícula, dando como resultado
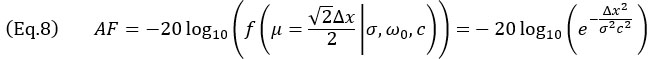
Una forma aproximada para el valor de Δx respecto de AF, en casos en los que el valor de AF es pequeño, que es el caso de uso típico para aplicaciones de NDT, puede obtenerse para el modelo oscilatorio de la Ecuación 7,

y el modelo de envolvente de la Ecuación 8,
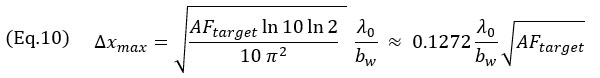
Estas expresiones traducen la dependencia de la raíz cuadrada del tamaño de la retícula en el valor de AF en todos los casos. La ecuación 9 se ha obtenido usando la aproximación de la serie Taylor de segundo orden de la Ecuación 7. Esta aproximación se ilustra en la Figura 6 además del modelo exacto. También podemos ver que el tamaño de la retícula para el modelo oscilatorio es casi independiente del ancho de banda relativo para bw pequeño. También cabe mencionar que, tanto para el modelo oscilatorio como para el de envolvente, la resolución máxima de la retícula Δxmáx está relacionada con la raíz cuadrada de la fidelidad de amplitud objetivo. Estos valores representan la resolución máxima de la retícula para el cumplimiento normativo basado en el modelo fenomenológico.
(a) El escenario de peor caso para TFM oscilatoria ocurre cuando el eje |
(b) El escenario de peor caso para la envolvente de TFM ocurre cuando el perfil de amplitud en |
Figura 5. Ilustración de la orientación del defecto relativa al eje ortogonal de la retícula para el escenario de peor caso, para (a) TFM oscilatoria y (b) envolvente de TFM.
Validación experimental
El modelo propuesto está validado con resultados empíricos en tres casos de uso de inspección de TFM diferentes. Para las tres configuraciones de TFM, se obtuvieron imágenes de varios SDH con resoluciones de retícula diferentes, y la fidelidad de amplitud se midió usando el método descrito anteriormente. Los parámetros de los tres casos de uso se describen en la Tabla 1. El primer caso está en contacto con una sonda de alta frecuencia (7,5 MHz), el segundo caso de uso emplea ondas rotacionales a una frecuencia inferior (5 MHz) y el tercero caso de uso emplea ondas rotacionales a una frecuencia superior de la sonda (10 MHz) y recuentos de elementos. Para todos los casos, los SDH están situados a 50 mm de la superficie superior de un bloque de acero de carbono.
Tabla 1: Parámetros de las configuraciones de TFM para la validación experimental de fidelidad de amplitud.
| Caja | Parámetros de la sonda | Parámetros de la suela | Parámetros de la pieza | Modo TFM | |||||
|---|---|---|---|---|---|---|---|---|---|
|
Frecuencia
MHz |
Número
[#] |
Emisión
[mm] |
Velocidad
[m/s] |
Ángulo
[°] |
Altura
[mm] |
Velocidad
cp - cs [m/s] |
SDH
Diámetro [mm] | ||
| 1 | 7,5 | 64 | 1,0 | n/a | n/a | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1,0 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 0,5 | T-T |
| 3 | 10 | 64 | 0,5 | 2330 | 36,1 | 11,0 | 3240 - 5890 | 1 | T-T |
La Figura 5 muestra la fidelidad de amplitud resultante para la TFM oscilatoria estándar (parte superior) y para la envolvente de TFM (parte inferior). Cada punto gris individual representa una combinación de caso de uso distinta, SDH y resolución de retícula. La fidelidad de amplitud estimada usando el modelo gaussiano explicado anteriormente se muestra con una curva plana negra. La línea de puntos de color rojo representa el límite de 2 dB conforme a la normativa.
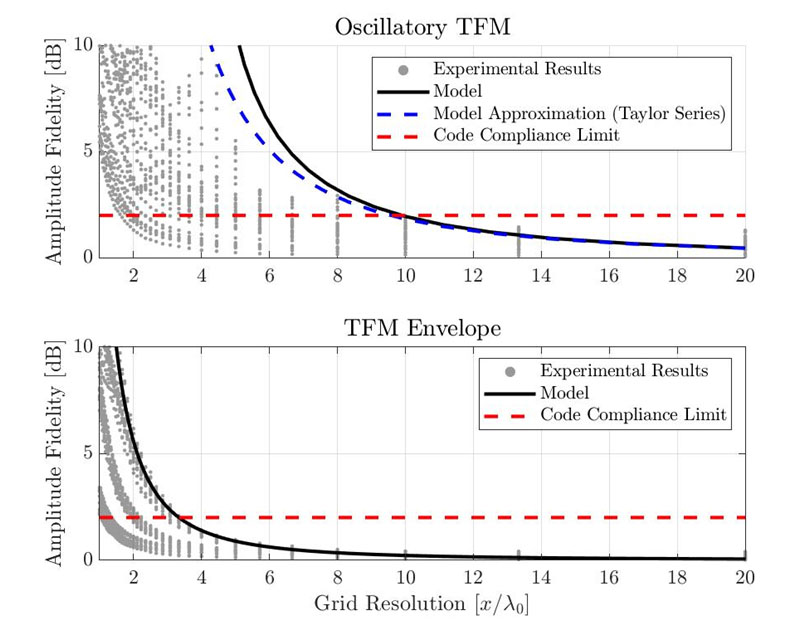
Figura 6. Comparación entre mediciones de fidelidad de amplitud empírica y resultados del modelo gaussiano propuesto para TFM oscilatoria estándar (parte superior) y envolvente de TFM (parte inferior).
Con el modelo propuesto, la resolución necesaria para cumplir la normativa es λ0/9,9 para TFM oscilatoria y λ0/3,3 para la envolvente de TFM. Los resultados experimentales muestran que la resolución mínima de la retícula para la conformidad normativa es de unos λ0/10 para la TFM oscilatoria y de λ0/3,3 para la envolvente de TFM. Cabe destacar, con todo, que esos valores se extraen del peor caso experimental presentado. Algunos de los valores de fidelidad de amplitud medidos son inferiores a 2 dB, incluso con una resolución de la retícula más gruesa. Por lo tanto, el modelo propuesto permite obtener buenas estimaciones, aunque conservadoras, para la fidelidad de amplitud de la configuración de TFM.
Conclusión
La fidelidad de amplitud de una configuración de TFM es una medida importante de la fuerza de una imagen en lo tocante a la resolución de la retícula. Cuanto más densa sea la retícula, más bajo será el valor de fidelidad de amplitud. Los códigos y los estándares ahora incluyen el método de focalización total como una nueva técnica de inspección y requieren una fidelidad de amplitud de 2 dB o menos. Este documento explica cómo puede medirse la fidelidad de amplitud correctamente de forma empírica y propone un modelo analítico simple para estimar la fidelidad de amplitud de los resultados para una configuración de TFM.
Se ha propuesto un modelo analítico simple basado en el perfil de amplitud en el eje principal de la propagación acústica. El modelo estima el perfil de amplitud como una oscilación del coseno gaussiano con modulación. La utilización de este perfil para estimar la fidelidad de amplitud permite obtener buenos resultados para TFM oscilatoria estándar y la envolvente de TFM. Los resultados empíricos mostraron la necesidad de obtener una resolución de retícula de hasta λ0/10 o λ0/3,3, respectivamente, para TFM oscilatoria estándar y la envolvente de TFM. El modelo analítico propuesto estima la necesidad de una resolución de retícula de λ0/9,9 para TFM estándar y de λ0/3,3 para la envolvente de TFM. Por lo tanto, el modelo propuesto podría usarse para eliminar la fidelidad de amplitud de la configuración de TFM.
Para obtener más información sobre las ventajas de usar la envolvente de TFM como parte de una solución conforme a la normativa, lea el informe técnico "Utilización del método de focalización total con la función de envolvente".
Bibliografía
[1] ASME Committee, 2019, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.”
[2] Oralkan, O., Ergun, A. S., Johnson, J. A., Karaman, M., Demirci, U., Kaviani, K., Lee, T. H., and Khuri-Yakub, B. T., 2002, “Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging?,” IEEE Trans. Ultrason., Ferroelect., Frec. Contr., 49(11), pp. 1596–1610.
[3] Thomenius, K. E., 1996, “Evolution of Ultrasound Beamformers,” 1996 IEEE Ultrasonics Symposium. Proceedings, IEEE, San Antonio, TX, USA, pp. 1615-1622.
[4] Freeman, S., Li, P., and O’Donnell, M., “Retrospective Dynamic Transmit Focusing,” p. 24.
[5] Wilcox, P. D., 2006, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” AIP Conference Proceedings, AIP, Brunswick, Maine (USA), pp. 845-852.
[6] Portzgen, N., Gisolf, D., and Blacquiere, G., 2007, “Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54(1), pp. 118-127.
[7] Sharpe, R. S., ed., 1982, Research Techniques in Nondestructive Testing. Vol. 6: ..., Acad. Press, London.
[8] Holmes, C., Drinkwater, B. W., and Wilcox, P. D., 2008, “Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation,” Ultrasonics, 48(6–7), pp. 636-642.
[9] Holmes, C., Drinkwater, B. W., and Wilcox, P. D., 2005, “Post-Processing of the Full Matrix of Ultrasonic Transmit–Receive Array Data for Non-Destructive Evaluation,” NDT & E International, 38(8), pp. 701-711.
[10] ISO, «ISO/DIS 2020 -FMC-TFM - General Use of TFM-FMC Technique [ISO / DIS 23865 -FMC-TFM - Uso general de la técnica TFM-FMC]»,
[11] Johnson, P., 2019, “With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections.,” Code Compliant TFM Weld Inspection with Three Clicks.
[12] ASME Committee, 2019, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture.”
![[a]](https://static5.olympus-ims.com/modules/imageresizer/a70/039/163421b9f1/330x281p200x170.jpg)
![[b]](https://static4.olympus-ims.com/modules/imageresizer/786/361/f1b5eaf50f/330x281p200x170.jpg)
![[c]](https://static5.olympus-ims.com/modules/imageresizer/acb/b8f/84e22aa03f/330x281p200x170.jpg)
![[a]](https://static5.olympus-ims.com/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_17.jpg?rev=9D7F)
![[b]](https://static1.olympus-ims.com/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_18.jpg?rev=D476)