2.5 Dynamique du front d’onde
Formation du front d’onde
Si une sonde monoélément peut être considérée comme un piston, un seul disque ou une plaque poussée vers l’avant sur le matériau inspecté, le front d’onde qu’elle génère peut être modélisé mathématiquement comme la somme des ondes provenant d’un très grand nombre de sources ponctuelles. Cela découle du principe de Huygens, d’abord avancé par le physicien hollandais Christiaan Huygens au XVIIe siècle, qui stipule que chaque point sur un front d’onde qui avance peut être considéré comme une source ponctuelle générant une nouvelle onde sphérique, et que le front d’onde fusionné qui en résulte constitue la somme de toutes ces ondes sphériques séparées.
Étalement du faisceau
En principe, l’onde ultrasonore générée par une sonde se déplace en ligne droite jusqu’à ce qu’elle rencontre une limite matérielle. Ce qui en résulte est présenté ci-dessous. Mais si la longueur du parcours ultrasonore est supérieure à la longueur du champ proche, le faisceau augmente également de diamètre et diverge comme le faisceau d’un projecteur. L’angle de divergence du faisceau d’une sonde peut être calculé comme suit :

Dans cette équation, on constate que la divergence du faisceau augmente avec les fréquences basses et de petits diamètres. Un faisceau ayant un grand angle de divergence peut causer, sur la distance, une diminution rapide de l’énergie sonore par unité de surface et causer ainsi une diminution importante de l’énergie sonore des petits réflecteurs dans certaines applications comportant de longs parcours sonores. Dans ce cas, la réponse de l’écho peut être améliorée en utilisant une fréquence plus élevée ou une sonde de plus grand diamètre.
Atténuation
Lorsqu’il se déplace dans un milieu, le front d’onde organisé généré par une sonde à ultrasons commence à se détériorer en raison d’une transmission imparfaite de l’énergie dans la microstructure des matériaux. Les vibrations mécaniques organisées (ondes sonores) se transforment en vibrations mécaniques aléatoires (chaleur) jusqu’à ce que le front d’onde ne soit plus détectable. Ce phénomène est connu sous le nom d’atténuation acoustique.
La théorie mathématique de l’atténuation et de la diffusion est complexe. La perte d’amplitude due à l’atténuation dans un parcours ultrasonore donné est la somme des effets d’absorption, qui augmentent linéairement en fonction de la fréquence, et des effets de diffusion, qui varient dans trois zones selon le ratio de la taille des limites des grains ou d’autres diffuseurs par rapport à la longueur d’onde. Dans tous les cas, les effets de diffusion augmentent avec la fréquence. Un matériau donné à une température donnée, inspecté à une fréquence donnée, présente un coefficient d’atténuation spécifique, généralement exprimée en népers par centimètre (Np/cm). Lorsque ce coefficient d’atténuation est connu, les pertes dans un parcours sonore donné peuvent être calculées selon l’équation.

En pratique, dans les applications de CND par ultrasons, les coefficients d’atténuation sont généralement mesurés et non calculés. Dans tous les matériaux, les hautes fréquences s’atténuent plus rapidement que les basses fréquences ; par conséquent, on utilise généralement les basses fréquences d’inspection pour les matériaux à coefficient d’atténuation élevé, comme les caoutchoucs et les plastiques de faible densité.
Réflexion et transmission à partir d’une limite d’un plan perpendiculaire
Quand une onde ultrasonore traversant un matériau rencontre la limite d’un matériau différent positionné perpendiculairement par rapport aux ondes, une partie de l’énergie des ondes est réfléchie vers la source et l’autre partie poursuit son parcours. Le pourcentage de réflexion par rapport à la transmission est lié à l’impédance acoustique relative des deux matériaux, et cette impédance acoustique est elle-même définie comme la densité du matériau multipliée par la vitesse de propagation de l’onde ultrasonore. Le coefficient de réflexion à une limite plane et le pourcentage d’énergie sonore qui est réfléchie vers la source peut être calculé comme suit :

Cette équation permet de constater que plus les impédances acoustiques de deux matériaux se rapprochent, plus le coefficient de réflexion diminue ; inversement, plus les impédances acoustiques s’éloignent, plus le coefficient de réflexion augmente. En théorie, le coefficient de réflexion est nul sur les limites de deux matériaux ayant la même impédance acoustique, alors que le coefficient de réflexion se rapproche de 100 % sur les limites de deux matériaux d’impédance très éloignée (par exemple, l’acier et l’air).
Réfraction et mode de conversion sur les limites non perpendiculaires
Quand une onde ultrasonore traversant un matériau rencontre la limite d’un matériau à un angle autre que zéro degré, une partie de l’énergie des ondes est réfléchie à un angle égal à l’angle d’incidence. Simultanément, la partie de l’énergie des ondes émises dans le second matériau est réfractée selon la loi de Snell, qui a été dérivée de façon indépendante par au moins deux mathématiciens du XVIIe siècle. La loi de Snell concerne les sinus de l’angle incident et de l’angle de réfraction en fonction de la vitesse de propagation des ondes ultrasonores dans chaque matériau, comme le montre la figure ci-dessous.
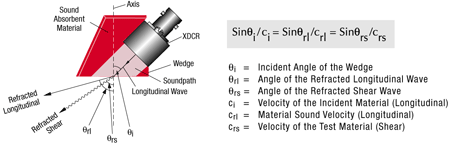
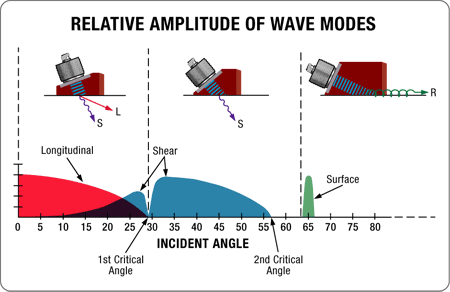
Si la vitesse de propagation dans le second matériau est plus élevée que dans le premier matériau, cette flexion s’accompagne d’un changement de mode au-dessus de certains angles, le plus souvent un passage du mode d’onde longitudinale au mode d’onde transversale. Il s’agit du principe de base des techniques d’inspection par faisceau angulaire largement utilisées. Quand l’angle d’incidence dans le premier matériau lent (par exemple, le sabot ou l’eau) augmente, l’angle de l’onde de réfraction longitudinale dans le second matériau rapide (par exemple, le métal) augmente aussi. Quand l’onde de réfraction longitudinale atteint près de 90 degrés, une partie de plus en plus importante de l’énergie des ondes est convertie en ondes transversales de faible vitesse réfractées à l’angle prévu par la loi de Snell. À des angles d’incidence plus élevés, ce qui générerait une onde de réfraction longitudinale de 90 degrés, l’onde de réfraction existerait uniquement en mode d’onde transversale. Un angle d’incidence encore plus élevé se traduira par une situation où l’onde transversale est théoriquement réfractée à 90 degrés, point auquel une onde de surface est générée dans le second matériau. Le diagramme ci-dessous illustre cet effet pour une sonde d’angle typique sur de l’acier.