Utilisation de l’imagerie par cohérence de phase pour la recherche de défauts

1. Introduction

Dans le domaine du contrôle non destructif (CND) par ultrasons, la méthode de focalisation en tout point (TFM) est désormais une technique d’imagerie largement connue et acceptée. Elle est maintenant offerte sur plusieurs appareils portables, y compris les appareils de recherche de défauts de la série OmniScan™ X3, et elle gagne en popularité au sein de la communauté du contrôle non destructif.

Cependant, bien que la TFM facilite l’interprétation des images par rapport à la technique classique d’inspection par ultrasons multiéléments (PA), l’utilisation d’un seul élément en émission lors de l’acquisition peut parfois donner lieu à des images ayant un faible rapport signal sur bruit. Ce faible rapport est attribuable à la mauvaise pénétration acoustique, qui survient généralement lors de l’inspection de pièces épaisses ou faites de matériaux à forte atténuation.

Pour régler ce problème, nous proposons ici une variante de l’algorithme TFM classique, laquelle utilise uniquement les informations relatives à la phase des signaux. Elle est fondée sur le facteur de cohérence vectorielle (VCF)¹, qui est utilisé comme une image en soi supprimant l’information d’amplitude des signaux acquis. Cette méthode, également appelée « imagerie par cohérence de phase » (PCI), présente certains avantages^2,3,4, notamment les suivants :

• Puisque seule la phase instantanée du signal est prise en compte² et que l’atténuation du matériau n’influence pas la phase du signal, la PCI peut être particulièrement utile pour résoudre les défis que présentent les applications d’inspection de matériaux épais ou à forte atténuation.
• L’amplitude du signal n’étant pas prise en compte, le besoin d’étalonner l’amplitude est éliminé.³
• Elle offre une sensibilité accrue aux formes diffractantes et une meilleure cohérence de la représentation des défauts entre les différentes vues de balayage.
• Elle fournit une méthode fiable, non fondée sur l’amplitude, pour le dimensionnement des fissures et des défauts similaires.³

Dans la suite de cet article, nous tenterons d’expliquer les principes de base de la technologie PCI d’Evident – dont une partie est en instance de brevet, notamment son procédé de production de représentations binarisées de signaux d’écho acoustiques. Toutefois, pour en venir à cette explication, nous examinerons d’abord le fonctionnement de l’algorithme de traitement du délai et de la sommation (DAS), qui permet de construire une image TFM classique avec enveloppe à partir de données FMC. Nous démontrerons ensuite que l’algorithme PCI constitue une variante de l’algorithme DAS.

Des exemples tirés de cas réels d’inspection de défauts artificiels de nature et de forme connues permettent de comparer les deux types d’images, soit les images de la TFM classique et de la PCI⁵ obtenues à l’aide des deux types d’algorithmes.

2. Examen des principes de la TFM classique et de l’algorithme DAS

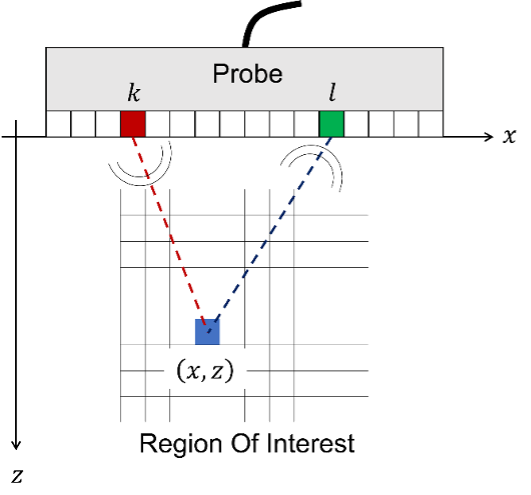
Figure 1. Configuration géométrique d’une acquisition FMC effectuée avec une sonde mise en contact avec la surface à inspecter.
L’élément piézoélectrique k émet une onde ultrasonore dans le matériau. L’élément piézoélectrique l reçoit l’onde ultrasonore réfléchie.

La figure 1 montre la configuration géométrique d’une acquisition de la matrice intégrale (FMC) effectuée au moyen d’une sonde d’inspection par ultrasons multiéléments (PAUT), ainsi que la région d’intérêt correspondant à la partie de l’échantillon à inspecter et à visualiser à l’aide de la TFM. L’élément piézoélectrique k émet une onde ultrasonore. Cette onde acoustique se propage ensuite dans le matériau de l’échantillon à inspecter, puis se réfléchit sur les éventuels défauts présents dans le matériau ainsi que sur les différentes interfaces. L’élément piézoélectrique l reçoit l’onde acoustique ultrasonore réfléchie, ce qui conduit à la formation du signal A-scan s_kl. La FMC regroupe ensuite tous les A-scans pour toutes les combinaisons kl.

La figure 2 montre un organigramme illustrant en six grandes étapes le principe de reconstruction par l’algorithme DAS (délai et sommation) d’une image TFM classique à partir d’une acquisition FMC :

1. L’acquisition FMC est effectuée, ce qui génère les données constituées de tous les A-scans s_kl^I (t). L’exposant I indique ici que ces A-scans sont les signaux en phase.
2. La transformée de Hilbert est appliquée, ce qui permet l’obtention des composantes en quadrature s_kl^Q (t) des A-scans s_kl^I (t) en phase acquis et regroupés dans les données FMC.
3. Les données x_kl^I et x_kl^Q sont extraites, et les délais précalculés τ_kl (x,z) y sont appliqués. Ces délais ont été précalculés en fonction du mode sélectionné (par exemple, LL, TT, TT-T, TT-TT) et de la région d’intérêt à observer.
4. La sommation permet alors l’obtention de deux images TFM en quadrature, soit I_TFM^I (x,z) et I_TFM^Q (x,z).
5. L’amplitude (aussi appelée « module » ou « enveloppe ») I_TFM (x,z) est estimée à l’aide du calcul de la distance euclidienne.
6. Ensuite, une étape de post-traitement, rendue possible grâce à la carte graphique, formate l’image TFM essentiellement par filtrage numérique, rééchantillonnage et redimensionnement. Cette image est présentée à l’utilisateur sur l’écran de l’appareil.

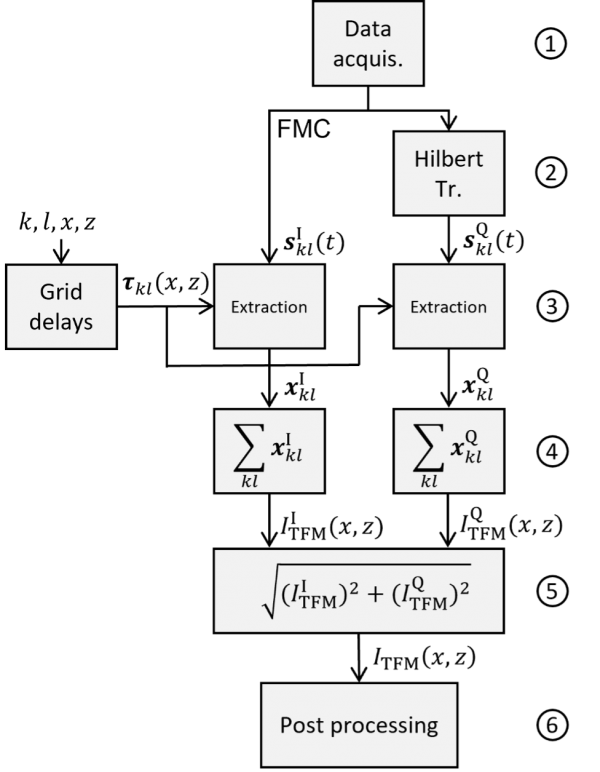
Figure 2. Principe de l’algorithme DAS en six étapes pour l’obtention d’une image TFM d’amplitude à partir d’une acquisition FMC

3. Principes de l’algorithme PCI

L’une des principales différences de l’algorithme PCI implémenté dans l’appareil de recherche de défauts OmniScan X3 64 par rapport à l’algorithme TFM classique et à d’autres technologies de traitement des signaux fondées sur la phase est qu’il a une composante novatrice de binarisation des signaux acoustiques (brevet en instance). Si l’on compare l’algorithme PCI à l’algorithme DAS – dont les étapes sont illustrées à la figure 2 – , il diffère sur deux points principaux :

• Il y a une étape supplémentaire, soit l’étape 3b (figure 4), qui consiste à quantifier les signaux s_kl^I (t) et s_kl^Q (t) en utilisant la fonction signe. Cette étape permet de mettre en évidence la cohérence des signaux, comme expliqué plus loin dans cet article.
• L’amplitude est calculée à l’aide de la norme L_∞, également appelée « norme de Tchebychev », au lieu de la norme euclidienne utilisée dans la TFM classique.

3.1. Concept de la cohérence de phase

Pour permettre une bonne compréhension de la nature de la PCI, il nous faut expliquer la notion de cohérence du signal, qui est un principe fondamental de cette méthode. Ce paragraphe décrit ce concept de façon simplifiée. Il faut d’abord accorder une attention particulière au fonctionnement de la fonction signe, parfois appelée « fonction signum ».

La fonction signe quantifie un signal s(t) sur 3 niveaux distincts, soit 1, 0 et -1 :

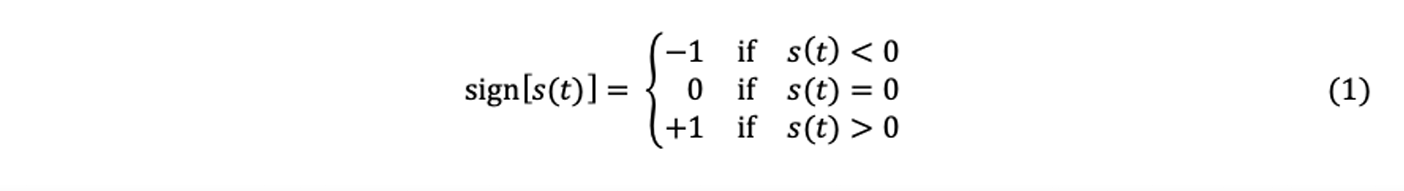
Pour mieux illustrer l’effet de cette opération de quantification sur les signaux, la figure 3 montre, à titre d’exemple, le résultat de l’application de la fonction signe sur un A-scan s(t), choisi ici arbitrairement à des fins de démonstration. En observant la figure 3, on peut noter ce qui suit :

• Le signal a deux types de zones : (1) des zones dites « cohérentes », qui indiquent la présence d’indications et qui sont symptomatiques de la présence de défauts, et (2) des zones dites « non cohérentes », qui indiquent l’absence d’indications et la présence de bruit pur. Il est à noter que ce bruit provient principalement du bruit électronique intrinsèque des équipements d’inspection, mais aussi du bruit structurel lié à l’interaction des ondes acoustiques avec le matériau inspecté.
• Dans les zones cohérentes, l’intensité du signal reste constante et comprise entre 1 et -1 dans le signal quantifié (figure 3(b)), tandis que l’amplitude décroît avec le temps dans le cas du signal brut (figure 3(a)) (en raison de l’atténuation géométrique, par exemple).
• Dans le signal quantifié de la figure 3(b), il y a un fort bruit présent, avec un aspect chaotique, à un niveau beaucoup plus élevé que le bruit presque imperceptible dans le signal brut de la figure 3(a). C’est ce qui explique pourquoi les images TFM obtenues avec la méthode PCI ont un aspect « plus bruyant » que les images TFM classiques, comme vous pouvez le voir en comparant les figures 6(a) et 6(b) ou les figures 8(a) et 8(b). Cependant, ces zones ayant des niveaux élevés de bruit chaotique (zones non cohérentes) ont une distribution statistique indépendante de la position dans l’image, contrairement aux zones cohérentes. En raison de cette différence, et malgré un aspect plus bruyant, il est plus facile de distinguer les zones cohérentes des zones non cohérentes dans une image générée par PCI. La palette de couleurs adaptée qui est appliquée par défaut dans l’appareil OmniScan X3 64 lors de l’utilisation de la PCI facilite cette distinction par l’utilisateur, comme illustré aux figures 6(c) et 8(c).

Le comportement de la fonction signe est donc utilisé en PCI⁵ d’une part pour maintenir une intensité de signal constante – quelle que soit la profondeur à laquelle on souhaite inspecter, par exemple – et d’autre part pour séparer les zones cohérentes indiquant probablement la présence de défauts des zones chaotiques non cohérentes indiquant une absence de défauts. Il est à noter que la cohérence des signaux est une information contenue dans la phase du signal.

D’un certain point de vue, les informations communiquées par la PCI peuvent être considérées comme de nature quasi-binaire, en ce sens que « cohérence/non-cohérence » équivaut à « présence d’un défaut/absence de défauts ». Le problème consiste alors à adopter une stratégie séparant ces deux régimes. Les manières dont cela peut être accompli ne sont pas abordées dans le présent article, mais une carte de couleurs adaptée, comme celle appliquée dans l’appareil de recherche de défauts OmniScan X3 64, facilite la tâche de séparation.

Figure 3 : Signal brut de type A-scan et bruit (a) / Signal quantifié à l’aide de la fonction signe (b)

3.2. Algorithme PCI

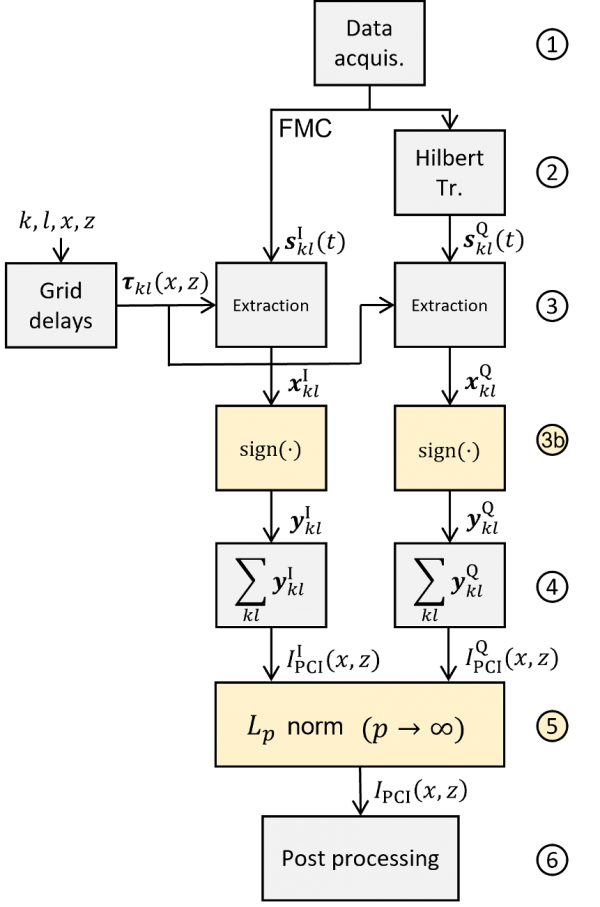
Figure 4. Principe de l’algorithme PCI

L’organigramme de la figure 4 résume comme suit l’algorithme PCI implanté dans l’appareil de recherche de défauts OmniScan™ X3 64 :

1. Phase d’acquisition qui génère les données FMC constituées de tous les A-scans s_kl^I (t). L’exposant I indique que ces A-scans sont les signaux en phase.
2. Application de la transformée de Hilbert, laquelle permet l’obtention des composantes en quadrature s_kl^Q (t) des A-scans s_kl^I (t) en phase acquis et regroupés dans les données FMC.
3. Extraction des données x_kl^I et x_kl^Q au moyen des délais τ_cl (x, z). Ces délais ont été précalculés en fonction du mode sélectionné (par exemple, LL, TT, TT-T, TT-TT) et de la région d’intérêt à observer.

Ces trois premières étapes sont identiques à celles de l’algorithme DAS de la figure 2.

3b. Quantification des signaux x_kl^I et x_kl^Q au moyen de la fonction signe selon l’équation 1, qui conduit aux signaux y_kl^I et y_kl^Q :

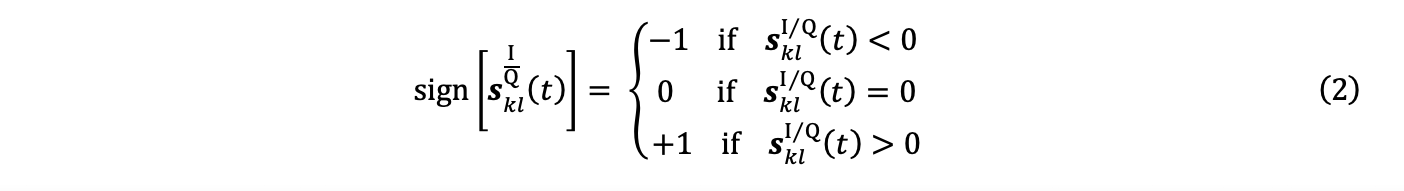
L’étape 3b est une étape supplémentaire propre à l’algorithme PCI.

4. La sommation donne lieu à deux images PCI en quadrature, soit I_PCI^I (x,z) et I_PCI^Q (x,z) :

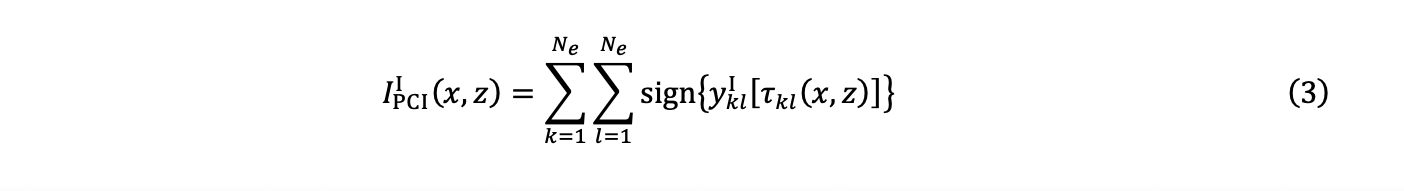
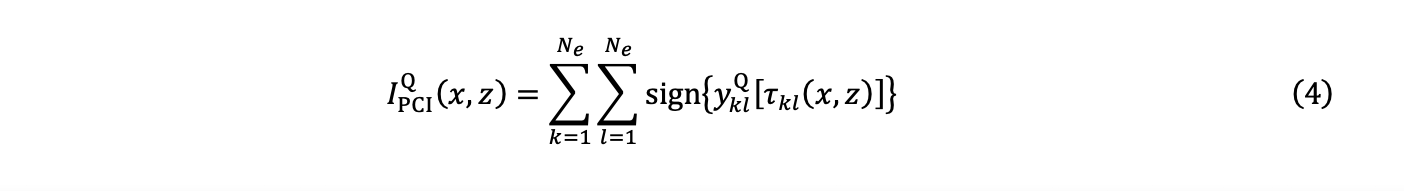
5. Ensuite, l’amplitude I_PCI (x,z) est estimée à partir du calcul de la distance de Tchebychev, aussi appelée « norme uniforme » ou « norme L_∞ », et des deux composantes des équations (3) et (4) :

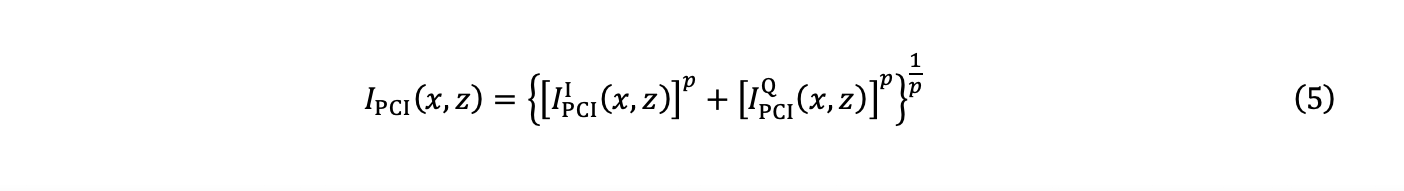
avec p→∞.

L’estimation de l’amplitude à partir de l’équation 5 est difficile à réaliser avec p→∞. Une bonne approximation peut alors être obtenue au moyen de l’expression suivante :

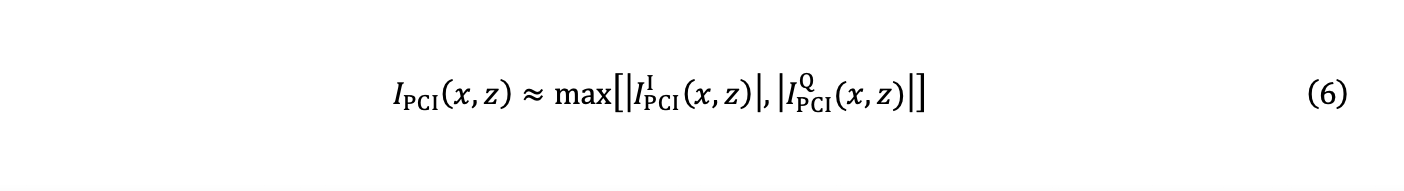
c’est-à-dire, en retenant comme valeur finale le maximum des valeurs absolues (|⋅|) des images en phase et en quadrature.

6. Enfin, il y a une étape de post-traitement rendue possible grâce à la carte graphique et identique à celle de l’algorithme DAS utilisé pour obtenir une image TFM classique. Elle formate l’image TFM essentiellement par filtrage numérique, rééchantillonnage et redimensionnement. Cette image est présentée à l’utilisateur sur l’écran de l’appareil.

De l’acquisition des données jusqu’à la génération des images pendant l’inspection, le processus de traitement PCI en temps réel illustré à la figure 4 et mis en œuvre dans l’appareil de recherche de défauts OmniScan X3 64 est effectué relativement à la même vitesse que le processus de traitement du mode TFM classique de l’appareil.

4. Exemples expérimentaux

Vous trouverez ci-dessous deux exemples fondés sur des mesures expérimentales effectuées sur des défauts de natures et de formes connues. Ils sont présentés ici pour comparer les images obtenues à l’aide des deux algorithmes précédemment décrits et mettre en évidence certaines caractéristiques de la PCI, soit sa robustesse aux effets d’atténuation et d’amplitude et sa sensibilité aux pointes des défauts.

4.1. Exemple 1 : bloc avec trous percés latéraux (SDH)

Le premier exemple d’inspection vise à mettre en évidence la robustesse de la méthode PCI aux effets d’atténuation et d’amplitude. Un bloc d’acier contenant 17 SDH (bloc étalon en acier à faible teneur en carbone ASTM E2491) est inspecté sans sabot (c’est-à-dire que la sonde est en contact direct avec la pièce inspectée) à l’aide d’une sonde PAUT 5L64-A32. Cette configuration d’inspection est illustrée à la figure 5.

La figure 6 montre les images reconstruites avec la TFM classique (a) et la PCI (b et c). Le mode de propagation L-L a été utilisé pour l’inspection. Sur la figure 6, on peut clairement observer ce qui suit :

• Dans l’image PCI, tous les SDH sont affichés avec la même intensité, alors que dans l’image TFM classique, on perçoit l’effet d’atténuation sur les SDH inférieurs et l’effet de l’amplitude transmise par le faisceau sur les SDH supérieurs.
• Le niveau de bruit de fond est également plus élevé dans l’image PCI.

Comme la PCI est une méthode d’imagerie qui n’utilise pas l’amplitude, la sommation cohérente des signaux se produit indépendamment de l’amplitude des signaux, et produit ainsi des indications avec un niveau de contraste élevé.³

Figure 5. Configuration de l’inspection pour l’exemple 1 : sonde 5L64-A32 et bloc étalon en acier à faible teneur en carbone ASTM E2491

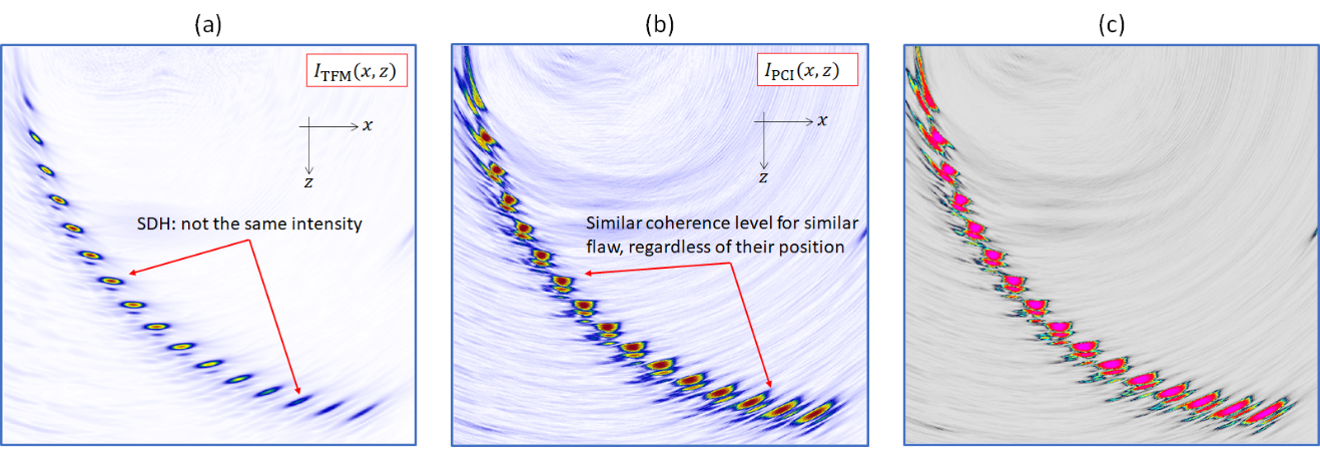
Figure 6. Images des SDH créées au moyen de la TFM classique (a), de la PCI (b), et de la PCI avec
la palette de couleurs par défaut appliquée dans l’appareil de recherche de défauts OmniScan X3 64 (c)

4.2. Exemple 2 : encoche dans un bloc d’acier

Une autre propriété intéressante de la PCI est sa sensibilité aux pointes des défauts, laquelle permet un dimensionnement précis des discontinuités. Il s’avère que les réflexions spéculaires provenant des grands diffuseurs sont réduites par rapport à la sommation d’amplitude, car seuls quelques termes de phase communs contribuent à la sommation. Ainsi, la PCI a tendance à être plus efficace pour les réflecteurs étroits et pointus.

Ce deuxième exemple a pour but de montrer cette caractéristique de la PCI. Il présente les résultats d’inspection obtenus avec un sabot SPWZ1-N55S-IHC et une sonde multiélément 7.5L60-PWZ1 sur un bloc d’acier comportant une encoche non débouchante orientée à 70°. La figure 7 montre la configuration de l’inspection.

La figure 8 montre les images reconstruites avec la TFM classique (a) et la PCI (b et c). Le mode de propagation TT-TT a été utilisé pour l’inspection. Les comparaisons suivantes peuvent être faites :

• Les réflexions spéculaires provenant des grands diffuseurs sont réduites par rapport à la sommation d’amplitude, car seuls quelques termes de phase communs contribuent à la sommation.
• Le contraste est amélioré lors de l’utilisation de la PCI par rapport à la TFM classique.
• La PCI offre une meilleure sensibilité aux pointes des défauts.
• Le rapport signal sur bruit est plus faible pour la PCI.

Ainsi, même si dans ce cas, une image TFM classique permet une évaluation plus précise de l’étendue de l’encoche, la PCI en permet le dimensionnement exact en raison de sa grande sensibilité aux pointes des défauts, et ne nécessite pas l’utilisation de facteurs semi-empiriques qui pourraient facilement être corrompus par un processus d’étalonnage ou une atténuation dans le matériau.

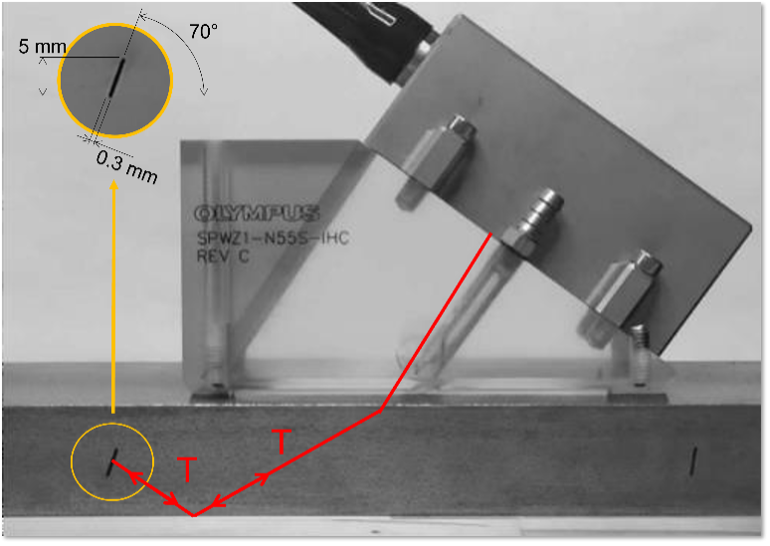
Figure 7. Configuration de l’inspection pour l’exemple 2 : sabot SPWZ1-N55S-IHC, sonde 7.5L60-PWZ1 et bloc en acier à faible teneur en carbone comportant une encoche angulaire produite par usinage par électroérosion

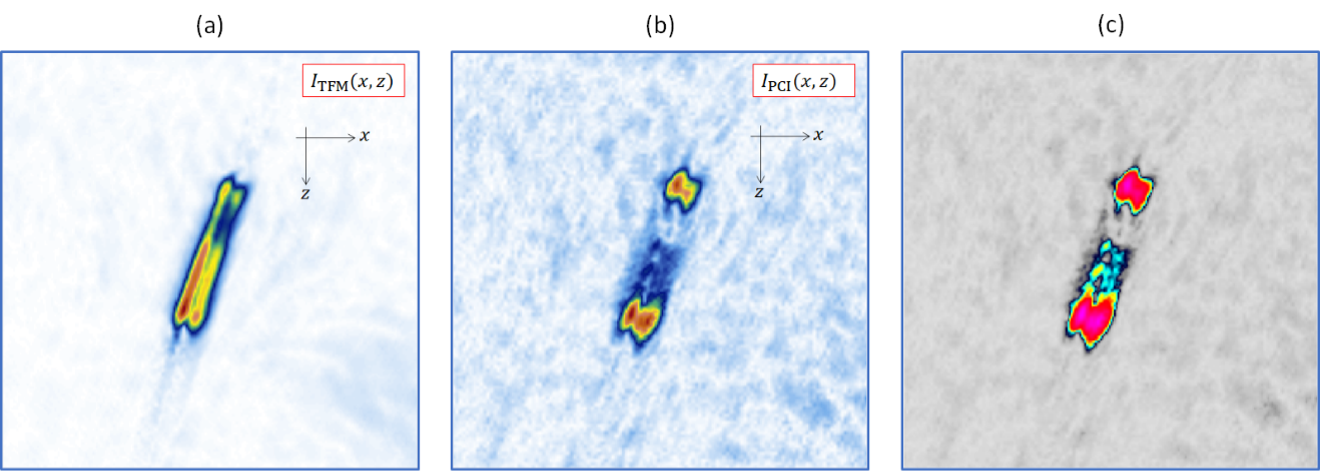
Figure 8. Images de l’encoche créées au moyen de la TFM classique (a), de la PCI (b),
et de la PCI avec la palette de couleurs par défaut de l’appareil de recherche de défauts OmniScan X3 64 (c)

Résultats expérimentaux

En conclusion, nos expériences ont montré que la PCI offre de nombreux avantages :

• Puisqu’il s’agit d’une méthode d’imagerie non fondée sur l’amplitude, l’interprétation des images n’est pas basée sur des signaux étalonnés en amplitude, ce qui est un avantage par rapport à la TFM classique fondée sur l’amplitude.
• La sensibilité est plus élevée pour les réflecteurs étroits et pointus, et de façon plus générale pour les formes diffractives.
• Elle permet un dimensionnement précis des défauts de type encoche sans utiliser de facteurs semi-empiriques qui pourraient être facilement corrompus par un processus d’étalonnage ou une atténuation dans le matériau.
• Elle ne nécessite pas de procédure d’étalonnage, ce qui rend le dimensionnement des encoches plus facile et plus précis par rapport à la TFM classique.
• Le gain peut être réglé sur une valeur très faible, ce qui évite la saturation du signal.
• Un appareil doté d’un processeur suffisamment puissant, comme l’appareil de recherche de défauts OmniScan X3 64, génère des images PCI en temps réel, de sorte que les résultats sont affichés immédiatement pendant l’inspection.

Toutefois, il nous faut mentionner certains inconvénients de cette méthode :

• La PCI reproduit mal les réflecteurs planaires.
• Le rapport signal sur bruit (SNR) de la PCI est inférieur à celui des méthodes fondées sur l’amplitude. Mais, comme expliqué précédemment, ce n’est pas un inconvénient majeur, car la PCI permet de distinguer facilement les zones cohérentes indiquant la présence de défauts des zones incohérentes indiquant les zones de bruit dans l’image.
• Les utilisateurs sont habitués de voir des vues d’extrémité fondées sur l’amplitude ; il peut donc y avoir une période d’adaptation.

Bibliographie

1. CRUZA, J.F., CAMACHO, J., FRITSCH, C. « Plane-wave phase-coherence imaging for NDE », NDT & E International, vol. 87, avril 2017, p. 31–37.
2. GAUTHIER, B., PAINCHAUD-APRIL G., LE DUFF, A., BÉLANGER, P. « Lightweight and Amplitude-Free Ultrasonic Imaging Using Single-Bit Digitization and Instantaneous Phase Coherence », IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control, vol. 69, n° 5, mai 2022, p. 1763–1774, doi : 10.1109/TUFFC.2022.3163621.
3. GAUTHIER, B., PAINCHAUD-APRIL G., LE DUFF, A., BÉLANGER, P. « Towards an Alternative to Time of Flight Diffraction Using Instantaneous Phase Coherence Imaging for Characterization of Crack-Like Defects », Sensors, vol. 21, n° 3, janvier 2021, p. 730, doi : 10.3390/s21030730.
4. LE DUFF, A., BADEAU N., PELOQUIN, E., PAINCHAUD-APRIL, G., KWAN, C.-H., GAUTHIER, B. « Total Focusing Method with Phase-Only Ultrasound Signal for Small Flaw Detection », International Ultrasonic Testing Conference (UT-Online), 2021.
5. PAINCHAUD-APRIL G., LE DUFF, A., KWAN C., BRILLON C. « Phase-Based Approach for Ultrasonic Inspection », World Intellectual Property Organization (WIPO). 02.09.2021. WO/2021/168565 https://patentscope.wipo.int/search/fr/detail.jsf?docId=WO2021168565=EP383773045