Uso del Metodo di focalizzazione totale con la funzione dell'Involucro
Nicolas Badeau1 Guillaume Painchaud-April1 Alain Le Duff1
1Olympus NDT Canada
3415 Rue Pierre-Ardouin
Quebec QC, G1P 0B3
Sintesi
Questo articolo tratta le modalità di calcolo dell'involucro di un'immagine TFM (Metodo di focalizzazione totale) e i vantaggi nell'uso di questo involucro TFM come soluzione per assicurare una conformità alle norme. L'involucro TFM è ottenuto calcolando la norma di due diverse immagini TFM, denominate come prima immagine TFM, calcolata mediante l'Acquisizione della matrice completa (FMC) standard, e una seconda immagine TFM, calcolata mediante l'FMC con trasformata di Hilbert. La risultante immagine dell'involucro TFM rappresenta una migliore base di riferimento per l'applicazione del metodo di misura basato sull'ampiezza in quanto è meno soggetta alle variazioni di ampiezza in confronto all'immagine TFM oscillatoria standard con un'identica risoluzione della griglia. Pertanto, riguardo alla TFM oscillatoria standard, può essere definita una risoluzione della griglia minore per l'involucro TFM. di conseguenza si riduce il complessivo sforzo di calcolo e, in definitiva, si aumenta la velocità di acquisizione risultante.
Introduzione
Il metodo di focalizzazione totale (TFM) rappresenta una tecnica recentemente accettata per la valutazione non distruttiva di materiali e strutture. Alcuni standard e norme adesso includono una parte relativa all'Acquisizione della matrice completa (FMC) e il TFM per i controlli non distruttivi (NDT) [1], [2].
Alcuni dispositivi NDT, come il rilevatore di difetti OmniScan™ X3, permettono di produrre immagini TFM in tempo reale. L'approccio TFM mediante l'FMC è sintetizzato nella prossima sezione, tuttavia la premessa fondamentale è che il TFM è basato sulla somma di numerosi valori di ampiezza degli A-scan elementari. Le immagini TFM sono oscillatorie a causa delle origini delle onde acustiche degli A-scan elementari. Al contrario, gli schemi di caratterizzazione delle applicazioni NDT sono essenzialmente delle tecniche basate sull'ampiezza per le quali l'andamento oscillatorio può essere interpretato come un artefatto acustico superfluo. Una pratica comune usata per adattare l'andamento oscillatorio agli schemi di caratterizzazione è quella di rettificare l'ampiezza, in modo che l'immagine appaia con dei valori rigorosamente positivi. Sebbene questo approccio possa facilitare l'interpretazione dell'immagine rispetto alla sua corrispondente completamente oscillante, questo articolo mostrerà come, usando l'involucro del segnale, potrebbe migliorare ulteriormente lo sforzo di caratterizzazione e aumentare la velocità di acquisizione in rapporto all'immagine TFM oscillatoria standard.
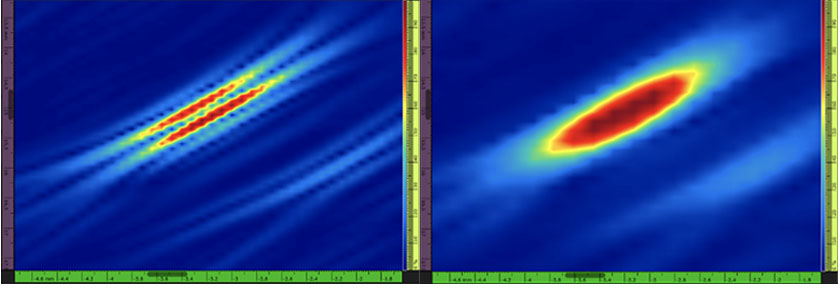
Figura 1 — A sinistra: Esempio di un'immagine TFM di un foro laterale (SDH - side-drilled hole) con valori di ampiezza rigorosamente positivi e oscillazione dei segnali (es. TFM standard). La risoluzione della griglia è di 0,08 mm (λ/8,1) e la massima ampiezza è di 108,7%. A destra: Involucro TFM dello stesso SDH La risoluzione della griglia è di 0,16 mm (λ/4,0) e la massima ampiezza è di 122,6%.
Esistono diversi svantaggi nell'uso di un'immagine TFM oscillatoria. Innanzitutto, la risoluzione della griglia TFM (es. la distanza tra due pixel nel frame) deve essere approssimativamente pari a λ/8 per essere conforme alle norme [1]–[3]. In questo articolo λ rappresenta la lunghezza d'onda associata con la frequenza centrale della sonda e la velocità acustica nella componente da ispezionare. Una ridotta risoluzione della griglia indica un consistente sforzo di calcolo, il quale si traduce immediatamente in una minore velocità di acquisizione. L'affidabilità associata ai metodi di misura dei difetti basati sull'ampiezza è inoltre influenzata dal TFM oscillatorio. Invece l'ampiezza massima di un'eco misurata è fortemente dipendente dall'offset del segnale acquisito.
Tutti questi limiti possono essere risolti mediante l'involucro TFM visto che è in grado di rimuovere le oscillazioni dei segnali nelle immagini e permette una misura dell'ampiezza massima più affidabile (vedi Figura 1). L'involucro TFM incide positivamente sulla produttività dell'acquisizione in quanto richiede una risoluzione della griglia ridotta (es. maggiore distanza tra due pixel adiacenti) per raggiungere la stessa affidabilità dell'ampiezza in confronto al TFM standard. Per esempio una risoluzione della griglia di approssimativamente λ/4 è sufficiente per l'involucro TFM per raggiungere la stessa affidabilità di ampiezza (2 dB) del TFM oscillatorio standard con una risoluzione di λ/8 [3].
L'obiettivo di questo articolo è di condividere i vantaggi nell'uso dell'involucro TFM con gli specialisti NDT. Innanzitutto faremo una sintesi sull'approccio FMC-TFM e in seguito riporteremo una breve presentazione dei concetti correlati al calcolo dell'involucro TFM. In seguito elencheremo i vantaggi nell'uso dell'involucro TFM, per assicurare una conformità alle norme, in confronto alle immagini TFM di tipo oscillatorio standard.
Sintesi sull'approccio FMC-TFM
Un elemento caratterizzante degli ultrasuoni phased array è la capacità di focalizzare nella componente da ispezionare in qualunque posizione desiderata. L'approccio con focalizzazione phased array si avvale di ritardi, sia in fase di trasmissione che di ricezione, per sincronizzare il tempo di volo di segnali a breve impulso sulla posizione di interesse. Nella zona di focalizzazione del campione, l'ampiezza totale del fascio acustico generato si riduce e la corrispondente risoluzione di rilevamento aumenta drasticamente [4]–[12].
Il TFM è uno sviluppo naturale di questa capacità: il TFM produce un fascio focalizzato attraverso la focalizzazione-orientazione phased array in ogni posizione di un'area di interesse in una componente da ispezionare e all'operatore è presentata solamente la serie di punti dei dati focalizzati altamente definiti [13]–[16]. Spesso l'area di interesse consiste in una griglia Cartesiana uniforme di tutti gli obiettivi di focalizzazione richiesti. Certamente realizzare questa focalizzazione in ogni posizione della griglia attraverso il convenzionale approccio di formazione dei fasci in termini fisici richiederebbe molto tempo a causa del tempo di propagazione acustico necessario per ogni posizione di interesse.
Visto che le tipiche onde acustiche a ultrasuoni per le applicazioni NDT sono lineari, la formazione dei fasci in termini fisici risultante dalla sovrapposizione dei campi acustici correnti per tutti gli elementi contribuenti per una data apertura, può essere imitata attraverso un processo post-acquisizione in base alla serie di dati di Acquisizione della matrice completa (FMC - full matrix capture). Il recupero della serie di dati FMC implica la registrazione del segnale da tutti gli elementi che compongono l'apertura in ricezione, mentre viene prodotta un'emissione acustica per ogni singolo elemento che compone l'apertura in trasmissione. Pertanto la serie di dati FMC sono costituiti dai numerosi A-scan elementari per tutte le combinazioni di elementi di trasmissione e ricezione.
Come nel caso del phased array focalizzato-convenzionale, ottenere l'ampiezza focalizzata da una determinata posizione di focalizzazione richiede l'esecuzione delle seguenti operazioni:
- Il calcolo del tempo di volo necessario per la propagazione acustica per raggiungere la posizione focale corrispondente a una posizione di interesse selezionata della griglia e ritornare indietro all'elemento di ricezione, per tutte le coppie di elementi in trasmissione-ricezione dell'apertura
- La selezione del punto dell'ampiezza corrispondente all'ottimale e completo tempo di volo in trasmissione-ricezione per tutte le coppie di elementi in trasmissione-ricezione dell'apertura
- La somma di tutti i punti dell'ampiezza selezionati in riferimento a tutti gli elementi contribuenti delle aperture di trasmissione e ricezione
- Il posizionamento della risultante ampiezza sommata in corrispondenza dell'iniziale posizione della griglia scelta
La ripetizione di queste operazioni per tutte le posizioni dell'area di interesse produce una mappatura dell'ampiezza per la quale tutti i valori di ampiezza corrispondono a un fascio focalizzato in trasmissione e ricezione. Questo metodo di usare i dati FMC per produrre una mappa di ampiezza focalizzata sull'area di interesse (es. l'area TFM) viene definito approccio FMC-TFM.
Modalità di calcolo dell'involucro TFM
Questa sezione descrive come l'involucro TFM viene calcolato mediante gli stessi A-scan elementari (FMC) acquisiti per il TFM standard. Si fa presente che l'involucro si manifesta fisicamente e non è solamente un algoritmo di regolazione dell'immagine. L'involucro nell'immagine TFM è strettamente correlato ai singoli A-scan costituenti. Innanzitutto, per illustrarne schematicamente il comportamento, il concetto di involucro è rappresentato mediante una serie temporale di impulsi gaussiani. Il processo è inoltre applicato a un A-scan empirico e su un frame TFM completo.
Il segnale a(t) corrisponde al segnale acquisito (es. l'equivalente di un A-scan elementare acquisito attraverso l'FMC) ed è, in effetti, la parte reale di un complesso segnale analitico z(t), il quale può essere scritto come:
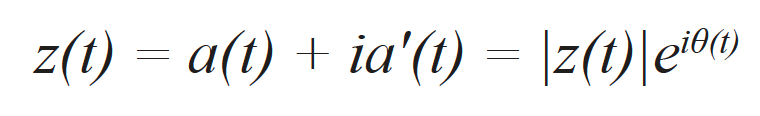
dove a’(t) corrisponde alla parte immaginaria del segnale analitico e θ(t) corrisponde alla fase istantanea del segnale. La parte immaginaria viene calcolata in modo efficiente mediante la trasformata di Hilbert [17]. L'involucro del segnale corrisponde alla norma del segnale analitico il quale può essere scritto come:
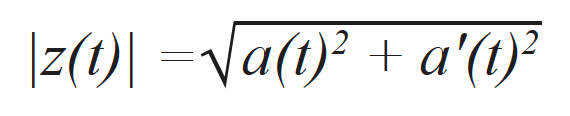
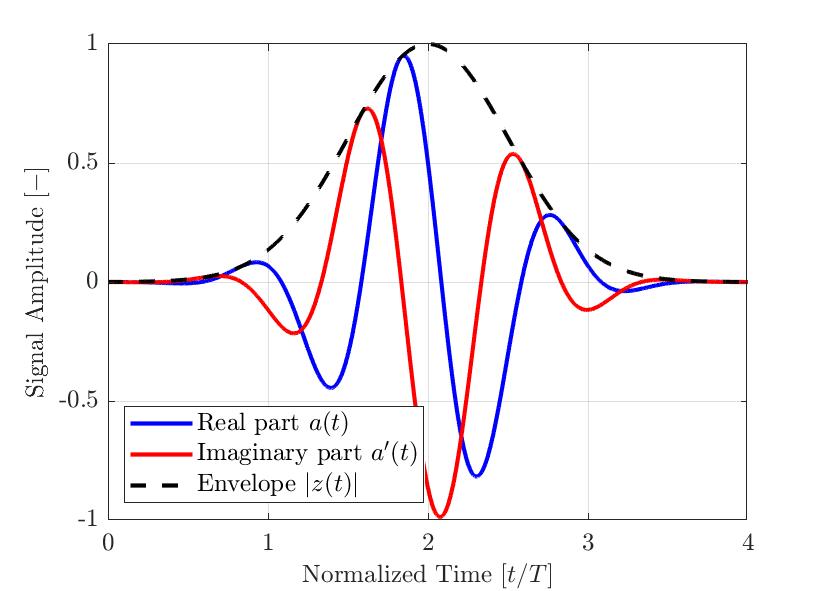
Figura 2 — Un tipico impulso modulato in base alla gaussiana per le applicazioni NDT. Illustrazione della parte reale, della parte immaginaria e dell'involucro calcolato. L'asse temporale è normalizzato con il selezionato periodo della frequenza centrale dell'impulso.
La Figura 2 mostra un esempio di un semplice impulso a(t) modulato in base alla gaussiana. Il segnale reale a(t) è in blu, la parte immaginaria della trasformata di Hilbert è in rosso e l'involucro risultante |z(t)| è una linea tratteggiata. Come visto nella precedente equazione, l'involucro del segnale |z(t)| non è influenzato dalla fase istantanea θ(t) del segnale. Pertanto segnali con diversi offset delle fasi ϕ possono avere lo stesso involucro. La Figura 3 illustra alcuni impulsi modulati in base alla gaussiana con diversi ϕ offset delle fasi e dell'involucro risultante. Pertanto l'ampiezza massima misurata del segnale è più affidabile quando si usa l'involucro del segnale rispetto al valore assoluto della parte reale del segnale analitico.
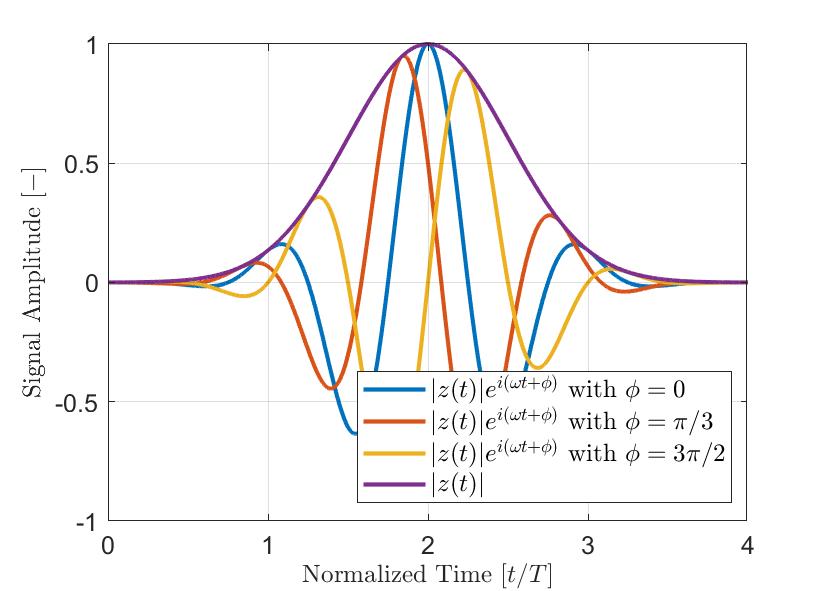
Figura 3 — Tipici impulsi modulati in base alla gaussiana (|z(t)|ei(ωt+ϕ)) con diversi ϕ offset delle fasi. L'involucro |z(t)| dei segnali è chiaramente indipendente dalla fase istantanea del segnale analitico.
Lo stesso processo può essere usato per ottenere l'involucro di un A-scan empirico. La Figura 4 mostra un tipico A-scan elementare acquisito attraverso l'FMC, mentre la Figura 5 mostra lo stesso A-scan (blu) con la rispettiva trasformata di Hilbert (rosso) e l'involucro calcolato (linea tratteggiata). Tutti i segnali illustrati sono normalizzati al massimo dell'involucro dell'ampiezza.
 Figura 4 — Parte di un A-scan elementare acquisito attraverso l'FMC. | 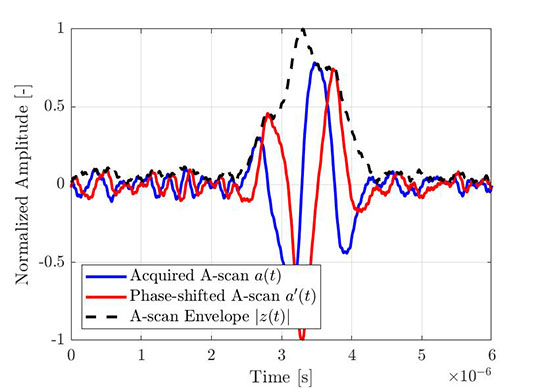 Figura 5 — Lo stesso A-scan elementare con la rispettiva trasformata di Hilbert e l'involucro calcolato. |
L'immagine dell'involucro TFM, con i singoli indici dei punti della griglia (k,l), viene calcolata mediante i segnali analitici provenienti da tutti i rispettivi A-scan contribuenti [15]. Infatti rappresenta il risultato del calcolo della norma di un'immagine TFM analitica y(k,l) composta dal frame TFM standard x(k,l), calcolata mediante i dati acquisiti FMC standard e un frame TFM x'(k,l) calcolato con la trasformata di Hilbert dei dati FMC. La stessa serie di ritardi viene usata in entrambi i casi. L'involucro TFM viene quindi calcolato mediante la seguente espressione
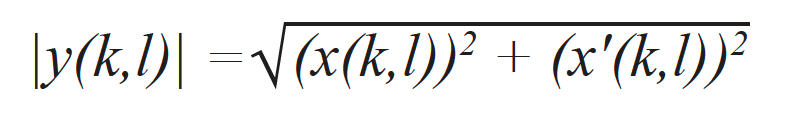
Un'immagine dell'involucro TFM è, pertanto, il risultato di un combinazione di due immagini TFM (vedi Figura 6): una dalla parte reale degli A-scan elementari e l'altra dalla parte immaginaria calcolata degli A-scan elementari. Sebbene questa procedura aumenti lo sforzo di calcolo e riduca la velocità di acquisizione dello strumento NDT, nella prossima sezione dimostreremo che la richiesta risoluzione della griglia può essere ridotta significativamente senza influenzare l'affidabilità dell'ampiezza, aumentando la velocità di acquisizione a un livello superiore rispetto a quando si usa il TFM standard.
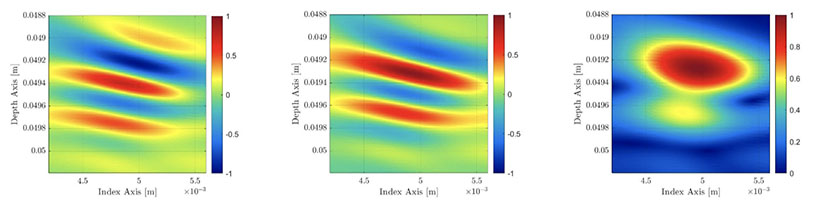
Figura 6 — A sinistra: Frame TFM standard (non in valore assoluto). Al centro: Frame TFM calcolato mediante la trasformata di Hilbert dell'FMC. A destra: Risultante immagine dell'involucro TFM.
Vantaggi nell'uso dell'involucro TFM
In questa sezione dimostreremo i vantaggi dell'involucro TFM confrontando alcuni frame TFM con diversi rapporti di risoluzione della griglia, compresi tra λ/9,3 e /4,0, e monitorando diversi metodi di misura di ispezione critici. I risultati sono stati ottenuti mediante una sonda 5L32-A31 e uno zoccolo SA31-N55S-IHC su un blocco di acciaio con un foro laterale (SDH - side-drilled hole) di 1 mm di diametro (vedi Figura 7). Tra lo zoccolo e il blocco di acciaio viene applicato un gel accoppiante (Sonotech Ultragel II) I dati sono acquisiti mediante il rilevatore di difetti Olympus OmniScan™ X3. Viene selezionato il percorso acustico impulso-eco (T-T) e la dimensione dell'area (20 mm × 20 mm). La lunghezza d'onda associata con la componente e il percorso acustico selezionati è pari a λ = 0,648 mm. La risoluzione della griglia è rappresentata in termini di frazione della lunghezza d'onda.

Figura 7 — Una foto della configurazione usata per acquisire le immagini TFM nella Tabella 1. Il rettangolo blu corrisponde all'intera area di interesse (20 mm × 20 mm) mentre il rettangolo rosso corrisponde all'area di interesse zoomata (5 mm × 5 mm) illustrate nelle immagini della Tabella 1. Abbiamo usato una sonda 5L32-A31 e uno zoccolo SA31-N55S-IHC. Il blocco in acciaio ha uno spessore di 40 mm.
La Tabella 1 mostra le risultanti immagini TFM per quattro diversi valori di risoluzione della griglia, compresi tra λ/9,3 a λ/4,0, sia per il TFM standard che per l'involucro TFM. Il valore calcolato di affidabilità dell'ampiezza [3] e la velocità di acquisizione risultante sono indicati in ognuna delle immagini TFM.
Risoluzione della griglia | TFM standard | Involucro TFM |
|---|---|---|
λ / 9,3 | 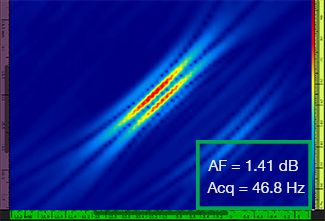 | 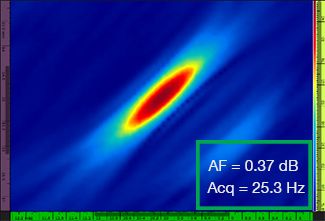 |
λ / 8,1 | 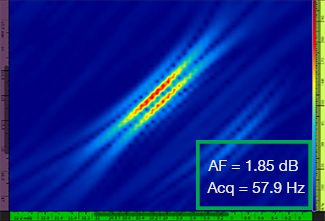 | 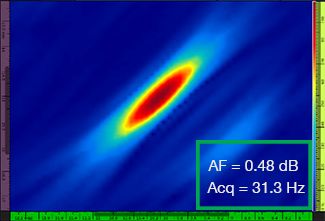 |
λ / 5,9 | 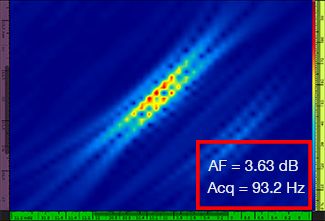 | 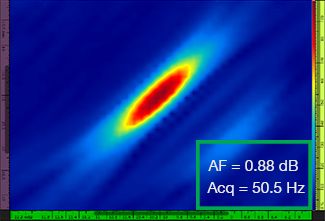 |
λ / 4,0 | 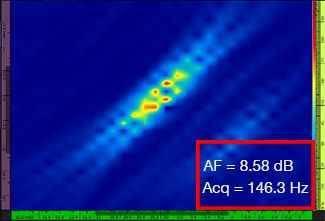 | 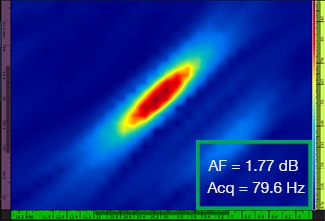 |
Tabella 1 — Confronto della qualità delle immagini tra il TFM standard e l'involucro TFM a quattro valori di risoluzione della griglia. Le immagini TFM sono zoomate in avanti. Nelle figure, AF significa affidabilità dell'ampiezza e Acq corrisponde alla velocità di acquisizione ottenuta con la risoluzione della griglia specificata. I rettangoli rossi indicano un mancato raggiungimento del valore di affidabilità dell'ampiezza di 2 dB conforme alle norme. Notare la maggiore velocità di acquisizione a un valore AF equivalente.
Recenti norme e standard [1, 2] richiedono il valore di affidabilità dell'ampiezza pari a 2 dB o inferiore. Pertanto, solamente i primi due valori di risoluzione della griglia (λ/9,3, λ/8,1) sono conformi alla norma quando si usa il TFM standard. L'involucro TFM permette una risoluzione della griglia minore (λ/4,0), conservando l'affidabilità dell'ampiezza in conformità alle norme. Di conseguenza, usando l'involucro TFM, con una risoluzione della griglia minore, è possibile un aumento della velocità di acquisizione di circa 37% in rapporto alla più elevata velocità di acquisizione raggiunta dal TFM standard conforme alle norme (57,9 Hz a λ/8,1).
Conclusioni
Il metodo di calcolo dell'involucro di un'immagine TFM è stato presentato e illustrato mediante esempi semplici. Abbiamo dimostrato che l'involucro di un segnale è indipendente dalla sua fase istantanea e, pertanto, assicura una base più affidabile per le tecniche di misura basate sull'ampiezza (come il metodo di diminuzione di 6 dB). L'involucro del segnale non rappresenta solamente una regolazione dell'immagine e non dovrebbe essere interpretato come un filtro, il quale potrebbe provocare la perdita di dati. I vantaggi nell'uso dell'involucro per l'acquisizione di immagini TFM sono stati dimostrati attraverso il confronto tra le immagini TFM, con e senza involucro, per diversi valori di risoluzione della griglia. Sebbene per ottenere il risultante involucro TFM devono essere calcolate due immagini TFM, lo sforzo di elaborazione può essere ridotto significativamente usando una minore risoluzione della griglia conservando la conformità alle norme. Questo è dovuto dall'affidabilità dell'involucro in rapporto alla variazione dell'ampiezza. Il risultato è un'immagine più idonea a una misura dell'ampiezza ma ottenuta a una velocità maggiore rispetto all'immagine equivalente elaborata mediante il TFM standard.
Bibliografia
[1] ASME Committee, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.” ASME, 2019.
[2] ASME Committee, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matric Capture.” ASME, 2019.
[3] N. Badeau, A. Le Duff e C.-H. Kwan, “Theoretical Model for Amplitude Fidelity Reading (submitted),” presentato al Simposio sulla ricerca ASNT, 2020.
[4] A. C. Clay, S.-C. Wooh, L. Azar e J.-Y. Wang, “Experimental Study of Phased Array Beam Steering Characteristics,” Journal of Nondestructive Evaluation, vol. 18, n°2, pag. 13, 1999.
[5] L. J. Bond, “Fundamentals of Ultrasonic Inspection,” ASM Handbook, vol. 17, n° Nondestructive Evaluation of Material, pag. 155–168, 2018.
[6] S.-J. Song, H. J. Shin e Y. H. Jang, “Development of an ultra sonic phased array system for nondestructive tests of nuclear power plant components,” Nuclear Engineering and Design, vol. 214, n°1–2, pag. 151–161, Maggio 2002, doi: 10.1016/S0029-5493(02)00024-9.
[7] S. Mahaut, O. Roy, C. Beroni e B. Rotter, “Development of phased array techniques to improve characterization of defect located in a component of complex geometry,” Ultrasonics, vol. 40, n°1–8, pag. 165–169, Maggio 2002, doi: 10.1016/S0041-624X(02)00131-2.
[8] S. C. Mondal, P. D. Wilcox e B. W. Drinkwater, “Design of Two-Dimensional Ultrasonic Phased Array Transducers,” Journal of Pressure Vessel Technology, vol. 127, n°3, pag. 336–344, Ago. 2005, doi: 10.1115/1.1991873.
[9] S.-C. Wooh e Y. Shi, “Influence of phased array element size on beam steering behavior,” Ultrasonics, vol. 36, n°6, pag. 737–749, Apr. 1998, doi: 10.1016/S0041-624X(97)00164-9.
[10] Joon-Hyun Lee e Sang-Woo Choi, “A parametric study of ultrasonic beam profiles for a linear phased array transducer,” IEEE Trans. Ultrason., Ferroelect., Freq. Contr., vol. 47, n°3, pag. 644–650, Mag. 2000, doi: 10.1109/58.842052.
[11] R. Ahmad, T. Kundu, e D. Placko, “Modeling of phased array transducers,” The Journal of the Acoustical Society of America, vol. 117, n°4, pag. 1762–1776, Apr. 2005, doi: 10.1121/1.1835506.
[12] B. W. Drinkwater e P. D. Wilcox, “Ultrasonic arrays for non-destructive evaluation: A review,” NDT & E International, vol. 39, n°7, pag. 525–541, Ott. 2006, doi: 10.1016/j.ndteint.2006.03.006.
[13] P. D. Wilcox, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” in AIP Conference Proceedings, Brunswick, Maine (USA), 2006, vol. 820, pag. 845–852, doi: 10.1063/1.2184614.
[14] J. Zhang, B. W. Drinkwater e P. D. Wilcox, “Effects of array transducer inconsistencies on total focusing method imaging performance,” NDT & E International, vol. 44, n°4, pag. 361–368, Lug. 2011, doi: 10.1016/j.ndteint.2011.03.001.
[15] C. Holmes, B. W. Drinkwater e P. D. Wilcox, “Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation,” Ultrasonics, vol. 48, n°6–7, pag. 636–642, Nov. 2008, doi: 10.1016/j.ultras.2008.07.019.
[16] C. Holmes, B. W. Drinkwater e P. D. Wilcox, “Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation,” NDT & E International, vol. 38, n°8, pag. 701–711, Dic. 2005, doi: 10.1016/j.ndteint.2005.04.002.
[17] D. Gabor, “Theory of Communication,” Journal of the Institution of Electrical Engineers, vol. 96, pag. 429–441, 1946.