概要
どのような造形プロセスにも、表面形状の形成には限界があります。こうした限界の指標の一つとなるのが、クロスオーバースケールです。積層造形(Additive Manufacturing:AM)のプロセス変数調整や、表面テクスチャーの向上を目指したAM用ツールの開発にとって、このスケールを理解することは重要なポイントとなります。本ケーススタディーでは、AMプロセスで作成したポリマー面の形状測定値を評価しました。形状の性質が変化するクロスオーバースケールの判定には、長さと面のマルチスケール解析、および尺度関連の派生値を利用。マルチスケール解析では、個別の変数値の大小にかかわらず、有効な近似解を統一的に得られるように設計された技法を用います。
造形面は、縮尺を大きくすると滑らかに見え、小さくすると粗く見えます(Brown, 2000)。この変化の境目となる尺度を、スムース・ラフ・クロスオーバー(Smooth-Rough Crossover:SRC)と呼びます。
AMで作成した面と他の技法で造形した面には、ある意味において共通点があると言えます。比較的大きな形状要素は造形プロセス変数に、小さな形状要素は繊細なツールと材料との相互作用に影響される点です。一般的に粗さと称されるのは、積層ピッチに左右される、規則性の高い、規模の大きな特徴です。より微細な規模の特徴には、材料の溶着プロセス(押し出しと硬化)などが決定づける、非常に不規則なものがあります。
これまでのAM面に関する研究では、マルチスケール解析を用いてクロスオーバースケールを導き出すことはありませんでした(例:Ahn et al., 2009; Kechagias, 2007)。今回は、造形物の形状分析をして、形状の規則要素、不規則要素の周期性およびクロスオーバースケールを調べるにあたり、マルチスケール解析を用いました。そしてこの形状を、規則要素より小さな尺度で統計的に比較しました。
技法
 図1:パーツの拡大図(積層ピッチ330µmで作成した、傾斜面のある10mmの立方体) | 熱溶解積層方式ラピッドプロトタイピング装置、Dimension SST 1200ESを使用して、1辺が45°の角度で斜めに切り取られた形状の10mmの立方体(図1)を作成しました。積層ピッチは250µmおよび330µmです。この熱溶解積層方式では、半流動体にした熱可塑性のABSを押し出し、1層ずつ積み重ねてパーツを作成します(考察は2種類の積層ピッチについて実施)。まずパーツの表面となる層の外周を形成し、その後内部を充填します。熱溶解積層方式ラピッドプロトタイピングは「熱溶解積層法」(Fused Deposition Modeling、FDM)とも呼ばれ、モデリング、プロトタイピング、さらには最終的な製造にまで広く利用されている積層造形法(3Dプリント)です。今回は、プラスチック素材を溶かして連続的な輪郭を形成する熱可塑性樹脂押出法でプロトタイプ部品を作成しました。 |
100倍対物レンズを装備した3D測定レーザー顕微鏡OLS4100を用いて、側面、傾斜面および天面の3D測定を行いました。その3D画像をスティッチングし、広い領域を可視化します。初期サンプリング間隔は227nmとし、121×121µmの各測定エリアを測定しました。この初期サンプリング間隔は、後の統合作業時に修正しました。
層と層の間の狭い領域で特に生じやすい異常な突出、スパイク(輝度の低い領域で発生しがちな測定の乱れ)の除去には、解析用ソフトウェア、Mountains 7(Digital Surf社)のスロープフィルターを使用しました。このスロープフィルターは、測定された傾斜角がユーザー指定のしきい値(今回は87.5°)を超えた場合、当該データを除外してくれます。この方法を採用することで、他の測定結果に影響を与えずに、非現実的な突出を除外することができます。スパイクを除去した部分のデータは周囲の高さの平均値で置き換え、除去部分の測定値を平滑化しました。補正をするとはいえ、相対的長さや面積を著しく増加させてしまう異常な測定の歪みを除外する目的のものであるため、測定結果の有用性はかえって高まります。
測定領域は、表面に顕著で大きな不具合がある箇所を避けて選択し、統合した大きな領域からはこうした部分を排除して平均化を行いました。この作業には、Mountain 7を使用しました。同ソフトウェアは測定結果のレンダリングイメージ(図2)作成にも用いられています。
フラクタル解析ソフトウェア、Sfraxを使用して、輪郭、および積層に対して垂直な断面について、輪郭の相対的長さと面の相対的面積のマルチスケール評価(ASME, 2009)を行いました。これらの選択領域には、3層分の断面が含まれています(図2)。
線スケール解析では、異なる尺度で繰り返しタイリングを行うにあたって線分を使用し、輪郭の長さをスケール関数として決定しました(ASME, 2009)。線分の長さは尺度を表し、どのタイリングにおいても一定となります。各尺度での相対的長さは、輪郭の実測長と名目上の長さ、すなわち直線の長さとの比で決まります。相対的長さは、輪郭の長さからサンプリング間隔までの尺度範囲で計算しました。
相対的面積のマルチスケール評価、つまり面スケール解析は、選択した層の膨らみ部分を対象としました。面スケール解析は線スケール解析と類似しています。異なるのは、相対的長さではなく相対的面積を求める点です。輪郭[z=z(x)]の代わりに面積測定値[z=z(x,y)]をタイリングするため、線分ではなく三角形を用います(ASME, 2009; ISO 25178, 2012)。
選択領域において、すべての尺度で相対的面積と複雑性のマルチスケール鑑別テストを行いました(複雑性は尺度に基づく派生値で、相対的長さまたは面積のサンプリング間隔10個を用いて求めます。複雑性を見れば、尺度の変化に伴い相対的長さや面積がどのように変化するかが分かります)。図2で示したとおり、相対的面積とその複雑性は、積層1層の膨らみ頂部領域の測定箇所(192×192µm)から計算されました。形態の除去に使用したのは、Mountains 7の2番目のフィルターです。表面を統計的に比較できるようにするため、これらの領域をSfraxで4つのセクション(2×2)に分割。F検定で二乗平均比(Mean Square Ratio:MSR)を求め、それぞれの利用可能な尺度で相対的面積に基づいて表面を鑑別するための確実性レベルを決定する臨界値と比較しました(F検定でデータセット内の偏差をデータセット間の偏差と比較し、これらの偏差の有意性を検討します)。MSRは、スケールと対比してプロットしました。
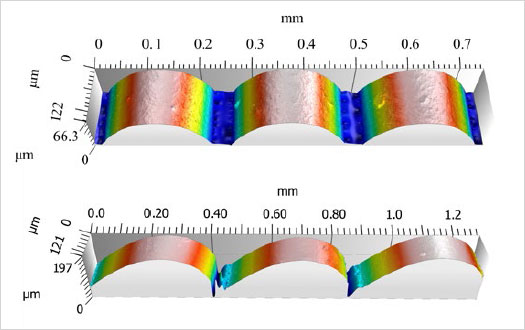
図2:積層ピッチ254µmにおける側面(上)と斜面(下)の表面測定結果のレンダリングイメージ
結果
図2は、積層ピッチ254µmの立方体の側面および斜面における、選択した表面の測定結果のレンダリングイメージです。図2では、積層ピッチに対応した規則的なパターンがはっきり表れています(イメージから簡単に積層ピッチを検出できます)。層と層の間の谷部の形状は、スパイクのフィルタリング後に高さを置き換え、平滑化されている点に注意してください。
表1に、4種類の面における従来型のパラメーター値を示しました。
| パラメーター | ||||||
| 高さ (µm) | ハイブリッド | |||||
| Surface | Sa | St | Sq | Sp | Sdq | Sdr % |
| 254µm側面 | 18.3 | 66 | 20.9 | 25.9 | 0.83 | 21.9 |
| 330µm側面 | 24.3 | 139 | 28.2 | 39.3 | 4.29 | 51.2 |
| 254µm斜面 | 37.1 | 159 | 43.5 | 49.7 | 2.22 | 58.4 |
| 330µm斜面 | 40.1 | 197 | 48.2 | 56.9 | 2.28 | 48.4 |
表1:ISO 25178に準拠した高さとハイブリッドのパラメーター(ISO, 2012)
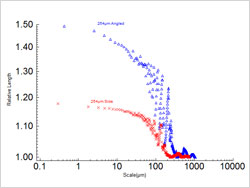 図3:積層ピッチ254µmの側面および斜面における相対的長さと尺度の分布 | 図3は、図2の側面および斜面から、縦方向、つまり積層に対して垂直方向の輪郭の相対的長さと尺度のプロットの分布を示したものです。相対的長さをマルチスケールで捉えることで、3つの異なる尺度領域が描出されます。約250µmおよび約350µmを超える大きな尺度では、側面および斜面共に相対的長さの変化は一定で、値は1付近にとどまっています。また、どちらの面でも、これらの大きい尺度から30µm近辺の尺度までの間に遷移領域があり、相対的長さが大きく不規則に増える傾向が見られます。30µm未満の尺度では相対的長さは増し続けますが、尺度を小さくしていくと、サンプリング間隔が300から400nmに到達するまで増加率は減少します。 |
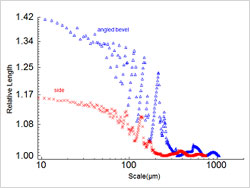 図4:積層ピッチ254µmの側面および斜面における相対的長さと尺度の分布(大きい尺度側の詳細) | 図4は、相対的長さの三つの領域の間に存在する二つのクロスオーバーを詳しく示したものです。最も大きな尺度では、相対的長さはわずかに伸び、その後再び1に近づいています。この現象は、尺度が小さくなるにつれて値が決定的に増加し始める前に、2回発生しています。相対的長さが決定的な増加を迎える前に1に近づいた時の最小尺度は、SRCの一種であると言えます(Brown, 2000; ASME, 2009; Brown et al., 1996)。図5は、SRC値をプロットしたものです。中間の尺度では、相対的長さの不規則性が波状になり、準周期性を示しています(「準周期性」とは、周期関数と類似点はあるものの、関数の厳密な定義を満たさないことを意味します。) |
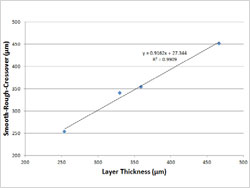 図5:スムース・ラフ・クロスオーバーと積層ピッチ、ならびに修正後の斜面ピッチの分布 | SRCは、修正後の積層ピッチに比例して直線的に増加しています(図5)。図5では、斜面の角度による相違を補正するために、斜面の積層ピッチに2の平方根[1/sin(45°)]を掛けて修正しました。その結果、積層ピッチとSRCには、強い相関性があることが明らかになりました。回帰係数(R²)は、0.99より大きく、傾斜は約0.9で、インターセプトはSRCの平均値の10%未満です。図5のようにプロットすれば、表1の高さパラメーターも単調増加となります。こうしたSRCとの傾向の類似性は、SRC同様、これらの高さパラメーターが大きい尺度の測定に強く影響を受けるという前提で一貫しています。ハイブリッドパラメーターは小さな尺度に最も大きな影響を受けやすく、修正後の積層ピッチと同様の増加は見られません。 |
図6は、積層ピッチ254µmと330µmそれぞれについて、得られた尺度すべてにおける側面と斜面の線スケールの複雑性を比較したものです。どちらのピッチでも、斜面のほうが側面より複雑性が高い傾向にあることが分かります。また、すべてのケースにおいて、尺度が小さくなると複雑性が顕著に減少しています。しかし、最も小さなスケールにおいては、複雑性の共通傾向に一貫したエビデンスは得られませんでした。
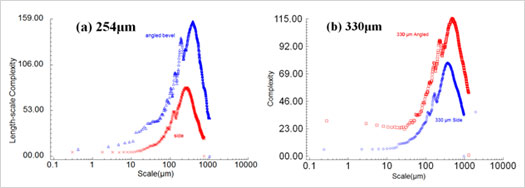
図6:積層ピッチ254µm(左)と330µm(右)における線スケールの複雑性と尺度の分布
図7では、層の膨らみ頂部から取った面スケール解析で使用される表面のレンダリングイメージを示しました。図8に示したのは相対面積、すなわち選択した頂部領域の面マルチスケール解析結果と、面スケールの分布です。これらの解析における線スケールは相対的長さのSRCより大幅に小さく、最大約30µmでした。線スケールは、三角形の面スケールの平方根の1/2になります。すべての面において、形態除去後の相対的面積の値は最大尺度で1に近づきます。こうした領域では、形態除去後のSRCは約100μm²または5μmになります。相対的面積と尺度の大きなプロセス、つまり積層ピッチや斜面との間の関係性は見られません。
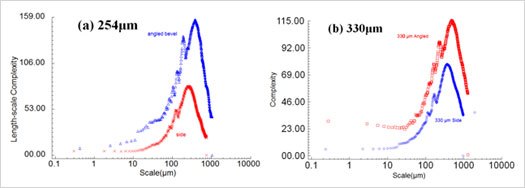
図7:積層ピッチ254µmの頂部から形態を除去して抽出した側面(上)および斜面(下)の領域
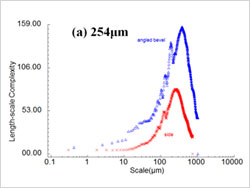 図8:全面から選択した膨らみ頂点における相対的面積と尺度の分布 | 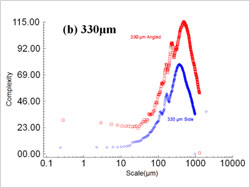 図9:選択領域における面スケールの複雑性とスケールの分布。どの面も、複雑性の最大値は0.4から20μm² |
 図10:積層ピッチ254µmおよび330µmの側面(上)と斜面(下)の面スケールの複雑性と、選択頂部の尺度からのマルチスケール鑑別の分布 | 図10は、各尺度の複雑性に対してF検定を使用したマルチスケール鑑別テストの結果です。二乗平均比(Mean Square Ratio:MSR)と尺度の分布をプロットし、99.9%の臨界MSRを示しました。MSRで示されるどちらの比較結果においても、鑑別能力は尺度約20μm²未満で一貫して高く、10μm²近辺で最大になります。その後、尺度が小さくなるにつれ低下します。MSR値が示すとおり、斜面より側面を鑑別する能力のほうが高くなっています(図10)。 |
謝辞
 3D測定レーザー顕微鏡 OSL4100 | 3D測定レーザー顕微鏡OLS4100をご提供くださったオリンパス社、そしてMountains 7をご提供くださったDigital Surf社に、深い謝意を表します。Sfraxソフトウェアを提供してくださったSurfract社は、共著者であるChristopher Brown博士が所有しています。 |
結論
熱溶解積層法で形成した部品の粗さを対象にしたマルチスケール解析は、異なる尺度で異なる形状の性質を特定する上で有効です。積層ピッチを整数倍した値が、線スケール解析における相対的最小値に対応します。積層ピッチをわずかに下回る尺度では、表面の形状に高い複雑性が見られます。数百nmから数十µmというごく小さな尺度では、数十µmから積層ピッチをわずかに下回るまでの大きな尺度と比べて、表面の複雑性が明らかに小さくなります。
ごく小さい尺度では、形状がプロセス変数に依存しないことが分かりました。なぜ同様の変化を見せないのか、理由は明らかではありません。このため、3種類の大きさに大別される積層ピッチの尺度からは除外しました。こうした尺度における粗さの形成は、積層ピッチによらず類似していると考えられます。ごく小さい尺度で相対的面積と類似していることが分かったハイブリッドパラメーター(Berglund et al., 2010)については、修正後の積層ピッチに含めていません。
粗さは、積層ピッチを狭めることで減少させることができます。図7で示したとおり、残る粗さは明らかにプロセスの他の側面に起因しており、積層ピッチを小さくしても排除することはできないと考えられます。
積層ピッチとSRCとの間の強い相関性は、旋盤の送り量とSRCの研究(Brown et al., 1996)で明らかになった関係と類似しています。旋盤の送り量や熱溶解積層法の積層ピッチより小さい尺度でも、形状に独自性があります。旋盤と熱溶解積層法のどちらにおいても、支配的なプロセス変数、つまり1回転あたりの送り量や積層ピッチと同じ尺度では、規則的な形状を示します。より小さな尺度では、形状が無秩序になります。
積層ピッチ前後の尺度で見られる相対的長さの準周期的な変化は、タイリングアルゴリズムと、より大きな尺度における積層形状の規則性との相互作用によるものです。積層ピッチの偶数倍の箇所で、エイリアシング(歪み)が明瞭に現れます。線スケールでは、タイリングアルゴリズムは形状の変化を考慮しないため、相対的長さの値は1へ向かいます。積層ピッチをわずかに下回る尺度では、タイリングアルゴリズムは、積層ピッチをさまざまに分画した値で準規則的な間隔と相互作用を起こします。
より小さな尺度において支配的なプロセス変数との相関性のエビデンスが不足しているのは、今回のサンプルサイズが小さいことと関連があるかもしれません。もし何らかの相関性があるとすれば、小さな尺度の形状形成にも積層ピッチが影響していると考えられます。本件と小さな尺度での形状形成メカニズムについては、本ケーススタディーの範囲外です。
本ケーススタディーの主な結論を要約すると、以下のとおりとなります。
1. 線スケールおよび面スケールのタイリングを用いたマルチスケール解析によって、明らかに異なる特性を持つ尺度領域を区別することができた。
2. 積層ピッチと同等以上の尺度における相対的長さは、強い規則性を示す。周期は、積層ピッチと面の方向に依存する。
2.1. 線スケールをプロットした場合、積層ピッチはスムース・ラフ・クロスオーバーの尺度と深く関係しているように見える。
2.2. 測定値から計算した斜面領域のスムース・ラフ・クロスオーバーは、積層ピッチにsine 45°を掛けた値に近い。
3. 層の膨らみ頂部における面スケールの複雑性は、20μm²未満の尺度においてパーツ間の差が顕著であった。
参考文献
Brown C A. Issues in modeling machined surface textures. Machining Science and Technology 2000; 4/3: 539-546.
Ahn D, Kim H, Lee S. Surface roughness prediction using measured data and interpolation in layered manufacturing. Journal of Materials Processing Tech. 2009; 209/2: 664- 671.
Kechagias J. An experimental investigation of the surface roughness of parts produced by LOM process. Rapid Prototyping Journal. 2007; 13/1: 17-22.
ASME B46.1. Surface texture: waviness, roughness and lay. New York: ASME; 2009.
ISO 25178-2, 2012. Geometrical product specifications (GPS) – Surface texture: Areal – Part 2: Terms, definitions and surface texture parameters.
Brown C A, Johnsen W A, Butland R M. Scale-sensitive fractal analysis of turned surfaces. CIRP Annals. 1996; 45/1: 515-518.
Berglund J, Brown C A, Rosen B-G, Bay N. Milled Die Steel Surface Roughness Correlation with Steel Sheet Friction, CIRP Annals. 2010. 59/1: 577-580.