저자: Nicolas Badeau, Guillaume Painchaud-April, Chi-Hang Kwan
요약
TFM(Total Focusing Method) 검사 기술은 이제 ASME 섹션 V와 같은 비파괴 검사(NDT)를 관리하는 코드 및 표준에 포함됩니다.TFM 스캔 계획을 위해 이러한 코드에 지정된 한 가지 중요한 매개변수 는 바로 진폭 충실도입니다.진폭 충실도는 이미징 그리드의 한정된 해상도로 인해 지정된 반사기에 대해 얻은 진폭 변화로 정의됩니다.이러한 코드에서 허용되는 일반적인 진폭 충실도 임계값은 최대 2dB입니다.코드에서는 주어진 설정에서 진폭 충실도를 측정하기 위해 실험적 방법을 제안하지만, 본 백서에서는 간단하고 보수적인 분석 방법을 제안합니다.TFM 엔벨로프를 사용하는 방식은 진폭 충실도 값이 설정된 허용 오차를 초과하지 않고 밀도가 낮은 TFM 그리드를 사용할 수 있도록 하여 진폭 충실도 추정에서도 사용이 고려됩니다.표준 TFM 이미징의 경우, 경험적 결과에 따르면 2dB 미만의 진폭 충실도를 얻으려면 약 λ0/10의 그리드 해상도가 필요합니다.엔벨로프를 사용하는 TFM 이미징의 경우, 경험적 결과에 따르면 코드를 준수하기 위해 λ0/3.3의 그리드 해상도가 필요합니다.
서론
TFM(Total Focusing Method)은 구성 요소의 비파괴 검사(NDT)를 위해 새로 채택된 기술입니다.ASME V[1]와 같은 표준과 코드에는 FMC(Full Matrix Capture)와 TFM이 추가적인 위상 배열 초음파 탐상 검사 기술로 통합되어 있습니다.FMC/TFM은 NDT 업계에서 비교적 새로운 기술이지만 의료용 초음파 이미징의 표준으로 의료 응용 분야에서 한동안 사용되었습니다[2~4].실제로 대부분의 의료용 초음파 이미징 기술은 일반적으로 벤치마킹되어 TFM 이미징과 비교됩니다.
FMC/TFM과 유사한 여러 기술이 존재하지만(예: VTFM[5], IWEX[6], SAFT[7]) 가장 일반적으로 사용되는 알고리즘은 시간 지연(delay-and-sum) 처리[2~4,8,9]입니다.FMC/TFM 기술은 송신기와 수신기 요소의 모든 조합에서 신호를 획득하는 수집 방식(FMC)과 관심 영역의 여러 위치에서 집속된 초음파 빔의 결과를 계산하는 합산 방식(TFM)으로 구성됩니다.TFM 관심 영역은 주로 데카르트 격자 위에 맞물려 있으며 음향 집속화가 적용되는 각각의 격자 교차점을 픽셀이라고 합니다.집속 방법은 FMC 데이터 매트릭스에 저장된 데이터를 사용하여 후처리에서 빔이 형성된다는 점을 제외하면 표준 위상 배열 초음파 이미징과 유사합니다.획득 후 시간 지연 프로세스는 일반적인 NDT 응용 분야에서 볼 수 있는 기본 음파의 선형성을 가정합니다.
FMC/TFM 기술은 기존 위상 배열 기술의 자연스러운 확장으로 볼 수 있습니다.그러나 기존의 위상 배열 초음파 탐상검사(PAUT)와 비교하면 데이터 표현의 차이로 인해 새로운 설정 매개변수를 고려해야 합니다.이러한 개념 중 하나가 TFM 그리드의 진폭 충실도(AF)입니다.AF는 TFM 그리드 해상도{Δx,Δz}로 인해 발생하는 지시의 최대 진폭 변화로 정의됩니다.균일한 데카르트 격자, 즉(Δx=Δz)는 이 연구의 나머지 부분에서 사용할 것을 고려합니다.진폭 충실도는 공식적으로 다음과 같이 표현할 수 있습니다.
![(식 1) AF(Δx)≡-20 log〖(A_(sampled max) (Δx))/A_(true max) 〗 [dB]](https://static3.olympus-ims.com/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_01.jpg?rev=17FA)
여기서 Asampled max는 유한 그리드 샘플링을 기반으로 관심 기능에 대해 측정한 최대 진폭이고, Atrue max는 무한 그리드 해상도를 기반으로 한 동일한 관심 기능의 최댓값입니다.Asampled max(Δx)의 두 축에서 그리드 크기가 0이 되는 한계는 Atrue max를 정의하고, 해당 진폭 충실도는 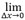 AF(Δx)=0이 됩니다.식 1은 그리드 해상도와 관련하여 진폭 충실도를 계산하기 위한 공식적인 정의를 제공합니다.그러나 실제로 기본 신호의 진정한 최댓값 Atrue max는 TFM 진폭 이미지의 오버샘플링과 보간법을 통해서만 추정할 수 있습니다.
AF(Δx)=0이 됩니다.식 1은 그리드 해상도와 관련하여 진폭 충실도를 계산하기 위한 공식적인 정의를 제공합니다.그러나 실제로 기본 신호의 진정한 최댓값 Atrue max는 TFM 진폭 이미지의 오버샘플링과 보간법을 통해서만 추정할 수 있습니다.
![(식 2) (AF) ̂(Δx)=-20 log〖(A_(sampled max) (Δx))/A ̂_(true max) 〗 [dB]](https://static5.olympus-ims.com/data/Image/white-papers/amplitudeFidelity/wpaper_amplitudeFidelity_02.jpg?rev=17FA)
여기서 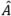 true max는 Atrue max의 추정치입니다.
true max는 Atrue max의 추정치입니다.
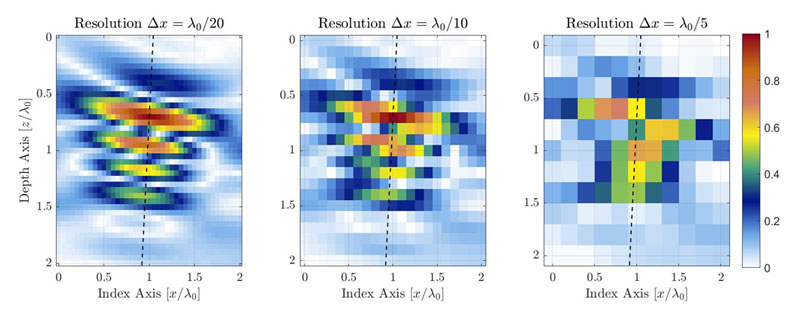
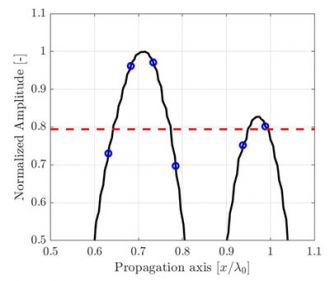
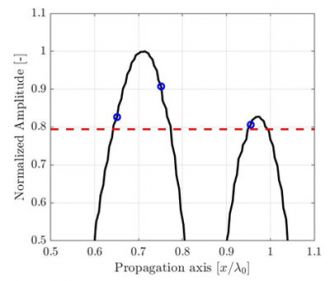
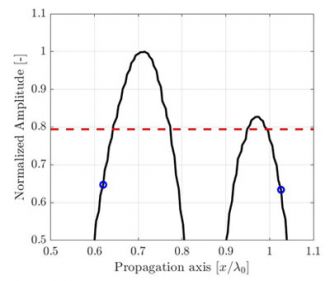
그림 1.TFM 그리드 해상도 감소로 인한 TFM 이미지 품질 저하 설명.점선은 음향 전파의 주축을 나타냅니다.
동일한 관심 영역의 경우 그리드 해상도가 낮을수록 픽셀 수가 더 적습니다.그림 1은 서로 다른 그리드 해상도 값에 대한 동일한 측면 드릴 구멍(SDH)의 일반적인 TFM 이미지를 보여줍니다.그리드 해상도는 프로브 중심 주파수 파장 λ0= c/f0의 일부로 정의됩니다. 여기서 c는 부품의 음향 속도이고 f0는 프로브 중심 주파수입니다.
이제 코드와 표준에는 진폭 충실도가 최대 2dB이 되어야 한다는 요구 사항이 포함됩니다[1,10].이 요구 사항은 적절한 NDT 분석을 충분히 보장할 수 있는 이미지 품질과 해당 관심 영역에 대한 TFM 그리드의 밀도에 크게 영향을 받는 검사 생산성 사이의 실용적인 절충안에서 비롯되었습니다.TFM 이미지 품질과 검사 생산성 간의 균형은 대량의 처리 능력에 액세스할 수 없는 휴대용 자율 장치에 특히 중요합니다.임베디드 하드웨어의 전력 효율성이 향상되고 원격 계산이 널리 보급됨에 따라 이 문제는 시간이 지나면서 사라질 것으로 예상됩니다.
일부 실증적 방법이 제안되었지만[10~12], 일반적으로 광범위한 계산이 필요하며, 그렇게 해서 얻은 결과는 그리드 해상도로 인한 실제 진폭을 나타내지 못합니다. 이 문제에 대해서는 다음 섹션에서 설명할 것입니다.이 백서에서는 NDT 기술자가 코드를 준수하고 생산적인 TFM 검사를 실시하는 데 도움이 되도록 TFM 설정에서 진폭 충실도를 정확하게 추정하는 방법을 제시합니다.
본 백서는 다음과 같이 나뉩니다.첫째, NDT 기술자가 직면한 문제에 대한 포괄적인 설명을 제공합니다.그런 다음 TFM 설정에서 진폭 충실도를 경험적으로 측정하는 방법을 설명합니다.다음 섹션에서는 진폭 충실도를 추정하기 위한 분석 모델을 제안합니다.그런 다음 제안된 모델을 세 가지 다른 TFM 사용 사례에 대한 경험적 측정과 비교합니다.그리고 완료된 작업을 포함하여 간단한 결론을 내립니다.
문제 사항
매우 미세한(즉, 밀도가 높은) 그리드에서는 매우 작은 진폭 충실도가 가능하지만, 실시간 TFM 이미지를 계산할 수 있는 최신 전자 기기에는 여전히 계산 한계가 있습니다.해당 관심 영역에 대한 그리드 해상도가 더 미세하다는 것은 계산할 초점이 많다는 것을 의미하며이에 따라 검사 생산성과 물리적인 스캐닝 속도가 감소합니다.NDT 기술자는 코드를 준수하면서 검사 생산성을 극대화하는 적절한 그리드 해상도를 선택할 수 있어야 합니다.
진폭 충실도는 다양한 주기에서 간단한 1차원 신호 샘플로 설명할 수 있습니다.그림 2 예에 나온 1차원 신호는 고해상도 λ0/100 이미지에서 가져온 음향 전파 축을 따라 그림 1에 제시된 SDH의 진폭입니다.신호 최대 진폭 근처의 확대된 부분만 예시 목적으로 제공됩니다.다시 말하지만, 세 가지 다른 해상도 λ0/20, λ0/10, λ0/5에서의 측정은 고해상도의 보간된 기준(일반 검은색 곡선) 위에 파란색 원으로 식별됩니다.
(a) 불연속 그리드 해상도는 λ0/20이고, 계산된 진폭 충실도는 AF = 0.27dB입니다. |
(b) 불연속 그리드 해상도는 λ0/10이고, 계산된 진폭 충실도는 AF = 0.82dB입니다. |
(c) 불연속 그리드 해상도는 λ0/5이고 계산된 진폭 충실도는 AF = 3.7dB입니다. |
그림 2.전파 축을 따라 기록된 진폭에 대한 샘플링 주기 효과에 대한 설명은 그림 1에 묘사되어 있습니다.1.시각적 이해를 돕기 위해 고해상도 보간 신호 기준(검은색 선)이 표시되어 있습니다.코드를 준수하는 2dB의 진폭 충실도는 빨간색 점선으로 표시됩니다.
분명한 결론은 식 1의 AF 값에 따라 정량화된 것처럼 밀도가 높은 그리드가 연속 신호를 더 잘 표현한다는 것이지만, 다음과 같은 최적화 문제가 여전히 존재합니다. TFM 이미지에서 가능한 모든 그리드 위치에 대해 목표값 AFtarget과 동일한 진폭 충실도 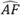 를 보장하는 최대 그리드 크기(Δxmax )는 얼마입니까?또는,
를 보장하는 최대 그리드 크기(Δxmax )는 얼마입니까?또는,
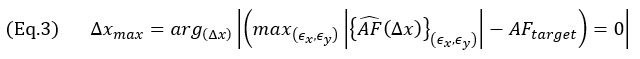
이러한 문제 제시로 볼 때, 고정된 셀 크기(Δx)에 대한 최대 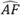 를 얻으려면 변위(ϵx,ϵy)로 식별되는 그리드의 모든 변환을 고려해야 한다는 것이 분명합니다.이는 TFM 이미지를 계산하기 위해 가능한 모든 그리드 배치 사례를 다루기 위함입니다.
를 얻으려면 변위(ϵx,ϵy)로 식별되는 그리드의 모든 변환을 고려해야 한다는 것이 분명합니다.이는 TFM 이미지를 계산하기 위해 가능한 모든 그리드 배치 사례를 다루기 위함입니다.
다음 섹션에서는 다중 그리드 변위 {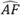 (Δx)}(ϵx,ϵy)에서 생성된 진폭 충실도 값에 대한 측정 원리를 설명합니다.
(Δx)}(ϵx,ϵy)에서 생성된 진폭 충실도 값에 대한 측정 원리를 설명합니다.
진폭 충실도의 경험적 측정
간단한 분석 모델을 사용하여 진폭 충실도를 추정할 수 있는 방법을 제시하기 전에 TFM 이미지의 경우 실험적으로 측정하는 방법을 정의하는 것이 가장 중요합니다.NDT 산업[10~12]에서 여러 기술이 설명되고 제안되었지만, 그 중 일부는 진폭 충실도를 완벽한 방법으로 정량화하지 않습니다.진폭 충실도의 경험적 측정 방식은 여러가지 정밀한 TFM 그리드 위치에서 많은 수의 TFM 이미지를 계산해야 한다는 점에서 NDT 기술자에게 데이터 수집에 대한 큰 부담이 될 수 있습니다.
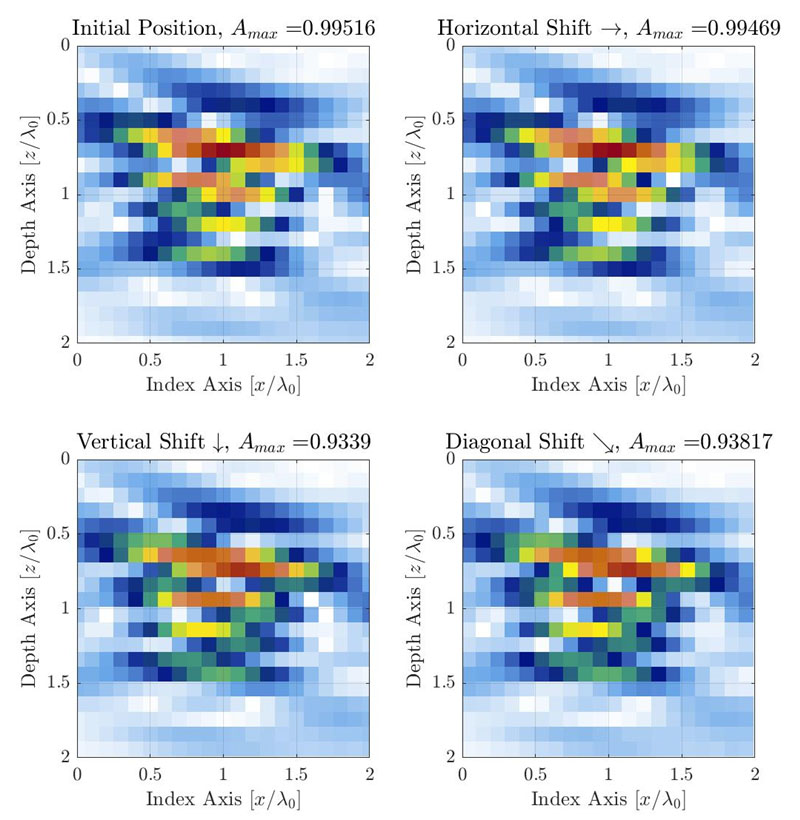
그림 3.그리드가 3가지 다른 방향으로 이동할 때 불연속 그리드 해상도로 인해 발생하는 AF 변화 설명.그리드 해상도는 Δx=Δy=λ0/10으로 설정됩니다.그리드는 오른쪽(ϵx=λ0/40,ϵy=0)(오른쪽 위), 아래(ϵx=0,ϵy=λ0/40)(왼쪽 아래)에서 그리드 셀의 1/4만큼 이동하고 대각선(ϵx=λ0/40,ϵy=λ0/40)(오른쪽 아래)에 있는 그리드 셀의 1/4만큼 이동합니다.
일반적인 TFM 응용 분야의 경우, SDH는 진폭 보정과 진폭 충실도 측정을 위한 기준 결함으로 사용됩니다[1,10].관측된 진폭은 관심 영역(즉, 프로브에 대한 TFM 그리드 위치)에서 프로브, 웨지, 대상 위치의 함수인 음향 전파의 주축을 따라 가장 많이 변합니다.그림 1에 설명된 사례에서 전파의 주축은 거의 수직입니다.그러나 일반적인 측정 방법의 경우 전파 축은 관심 영역 내의 위치에 따라 달라집니다.TFM 이미지의 경우 개별 그리드로 인해 발생하는 실제 진폭 변화를 포착하려면 샘플링 그리드를 모든 방향으로 이동해야 합니다.이 프로세스는 그리드 해상도가 λ0/10인 그림 1(가운데)의 동일한 예와 함께 아래에 설명되어 있습니다.
그리드 중첩을 얻는 데 필요한 횟수만큼 모든 방향에서 테스트할 그리드 해상도의 일부(예: 해상도의 약 1/20)만큼 그리드를 이동하는 것이 좋습니다.이는 두 개의 직각 방향에서 하나의 그리드 해상도 오프셋을 커버하기 위해 202 = 400의 전체 변위 단계가 필요함을 의미합니다(해상도의 1/20이라는 제안된 그리드 단계를 사용하는 경우).최대 진폭은 모든 그리드 오프셋에 대해 기록하며, 기록된 데이터의 최댓값 및 최솟값은 식 2를 사용하여 진폭 충실도를 얻는 데 사용합니다.그림 3에 제시된 사례에서 그리드 해상도는 λ0/10이고 측정된 진폭 충실도는 0.88dB입니다.필요한 변위 수로 판단할 때 NDT 기술자에게 이러한 수작업 과정은 번거롭고 시간이 오래 걸립니다.또한 단일 그리드 해상도의 진폭 충실도를 측정하기 위해 총 400개의 TFM 이미지를 계산해야 함을 의미합니다.
ASME 섹션 V[12]에서 제안된 대로 부품에 대한 프로브의 기계적 변위 대신 프로브에 대한 TFM 그리드 위치의 소프트웨어 변위를 사용하면 단일 FMC 데이터 세트를 사용하여 여러 TFM 이미지를 생성할 수 있습니다.이 접근 방식의 또 다른 이점은 그리드의 수직 구성 요소에 액세스할 수 있다는 것입니다.실제로, 프로브와 웨지는 깊이 축을 따라 선택한 SDH에 대해 기계적으로 이동할 수 없습니다.
일부 NDT 장치는 TFM 그리드를 이동하고 관심 영역에서 최대 진폭을 기록하고 궁극적으로 진폭 충실도 결과를 계산하는 반자동 도구를 손쉽게 제공합니다[11].그러나 이러한 도구는 일반적으로 그리드를 수평 방향으로만 이동시키기 때문에 결과적으로 진폭 충실도를 과소평가하게 됩니다.비교를 위해, 예를 들어 그림 3과 같이 그리드를 가로축으로만 이동하는 경우 진폭 충실도를 측정하면 0.06dB로 세로축을 고려하면서 측정한 진폭 충실도보다 15배 이상 낮습니다.
진폭 충실도 추정을 위한 현상학적 모델
이 섹션에서는 경험적 관찰에 기반한 간단한 분석 모델을 제안합니다.현상학적 모델은 대부분의 진폭 변동을 포함하고 따라서 그리드 해상도에 가장 민감한 전파의 주축을 따라 신호 동작을 고려합니다.그림 4는 기본 전파 축(파란색)과 빔 웨이스트 축(빨간색)을 따라 SDH의 TFM 결과 이미지의 경험적 프로파일을 보여줍니다.축의 원점은 엔벨로프 표현의 겉보기 최대 진폭 위치에 있으며 진동 표현에 대한 축 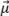 를 따라 작은 오프셋을 설명합니다.표준 진동 TFM 및 TFM 엔벨로프에 대한 프로파일이 제공됩니다.
를 따라 작은 오프셋을 설명합니다.표준 진동 TFM 및 TFM 엔벨로프에 대한 프로파일이 제공됩니다.
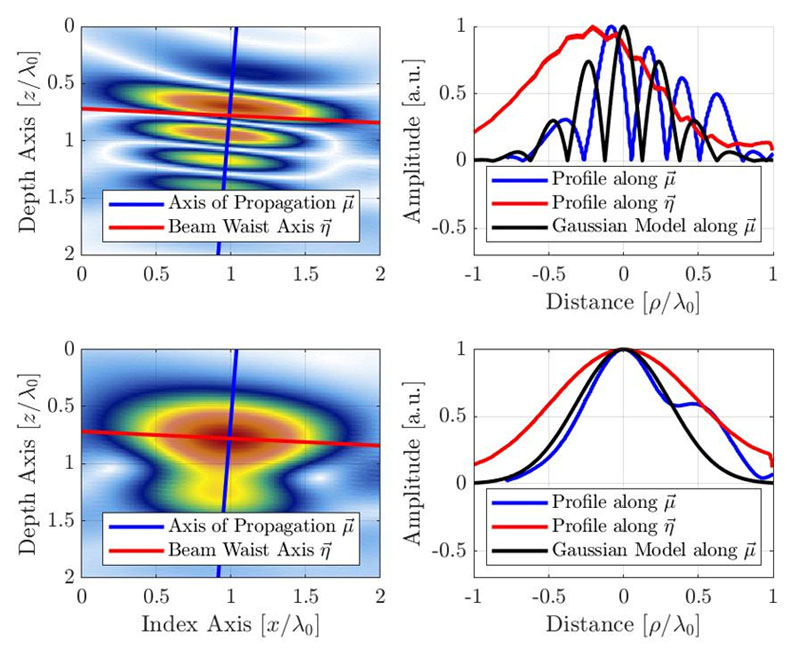
그림 4.음향 전파 축과 빔 웨이스트 축을 따라 신호 프로파일이 있는 TFM 이미지(상단: 진동, 하단: 엔벨로프).제안된 가우스 모델은 진동 및 엔벨로프 TFM 이미지에 대한 설명도 제공합니다.TFM 빔 형성의 펄스 에코 특성으로 인해 겉보기 파장이 절반으로 줄어듭니다.
이전에 언급한 바와 같이 최대 진폭 변화의 축은 음향 전파의 주축을 따르는 것으로 가정합니다.따라서 이 모델은 이 방향의 진폭 변화를 재현하는 것을 목표로 합니다.모델 신호는 변조된 가우스 코사인 신호입니다.
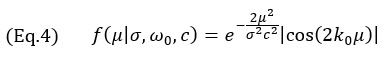
여기서 k0=ω0/c는 프로브의 중심 각 주파수 ω0에서의 파수이고, σ는 중심 주파수와 상대 대역폭 bw에 따라 달라지는 폭 매개변수입니다.폭 매개변수 σ는 다음을 사용하여 계산합니다.
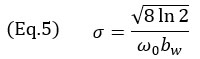
일반적인 NDT 위상 배열 프로브의 경우 상대 대역폭이 60%에 가깝기 때문에 (bw=0.6) 값이 모델에 사용됩니다.결국 이로 인해 가우스 엔벨로프가 단일 코사인 진동보다 더 크게 됩니다.식 3에서 코사인 항의 중심 주파수가 프로브 중심 주파수에서 두 배가 된다는 점은 특히 언급할 만합니다.이는 TFM 이미징(송신 및 수신 경로)의 펄스 에코 특성 때문이며 그림 4의 진동 사이의 거리에서 관찰할 수 있습니다.실제로 시간 도메인과 공간 도메인 간의 변환은 μ = tc/2로 나타냅니다.이는 또한 식 3의 지수항으로 사용되는 지수 2에 대해서도 설명합니다.
식 4의 진동 모델의 경우, 가우스 엔벨로프가 코사인 함수의 단일 진동보다 훨씬 크기 때문에 값이 클수록 AF에 대한 공간적 중첩이 생성되므로 |μ|≤λ0/8 값만 고려합니다.
TFM 엔벨로프 모델의 경우 식 4의 가우스 항만 사용되며 다음과 같이 산출됩니다.
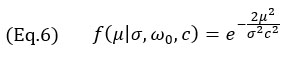
이는 모든 그리드 해상도에 유효합니다.식 3 및 식 7에서의 모델로 얻은 프로파일은 실험 프로파일과 함께 그림 4에 설명되어 있습니다.또한 경험적 측정에서는 메인 에코에 뒤처져 있는 표면파 신호(SDH의 전형적인 “랩 어라운드” 에코) 특징도 볼 수 있는데, 이는 제안된 모델에서는 누락되어 있는 것을 확인할 수 있습니다.
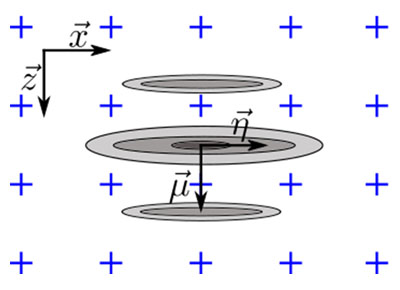
이 모델을 사용하여 진폭 충실도에서의 최악의 시나리오를 얻으려면 그리드 직각 축에 대한 결함의 방향을 고려해야 합니다.그림 5a에서 볼 수 있듯이 진동 TFM에 대한 최악의 시나리오는 음향 전파의 기본 축 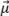 가 그리드 축 중 하나와 평행할 때 발생합니다.따라서 진폭 충실도는 최대 진폭이
가 그리드 축 중 하나와 평행할 때 발생합니다.따라서 진폭 충실도는 최대 진폭이 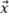 또는
또는 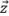 축을 따라 두 그리드 지점 사이의 중심에 있는 것처럼 계산해야 합니다.
축을 따라 두 그리드 지점 사이의 중심에 있는 것처럼 계산해야 합니다.
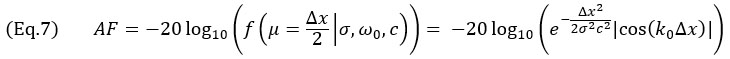
Δx≤λ0/4인 경우입니다.TFM 엔벨로프의 경우, 진폭 프로파일이 기본 전파 축 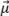 와 빔 웨이스트 축
와 빔 웨이스트 축 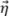 을 따라 동일한 경우 최악의 시나리오가 발생합니다.이 사례(그림 5b에 설명)는 SDH가 원으로 표시되는 경우에 해당하므로 전파 주축
을 따라 동일한 경우 최악의 시나리오가 발생합니다.이 사례(그림 5b에 설명)는 SDH가 원으로 표시되는 경우에 해당하므로 전파 주축 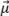 는 어떤 방향이든 가질 수 있습니다.최악의 시나리오는 그림과 같이 SDH 에코가 4개의 인접한 지점 사이에 집중될 때 발생합니다.이 사례에서 진폭 충실도는 그리드 대각선을 따라 계산해야 하므로 실질적으로 다음과 같이 산출됩니다.
는 어떤 방향이든 가질 수 있습니다.최악의 시나리오는 그림과 같이 SDH 에코가 4개의 인접한 지점 사이에 집중될 때 발생합니다.이 사례에서 진폭 충실도는 그리드 대각선을 따라 계산해야 하므로 실질적으로 다음과 같이 산출됩니다.
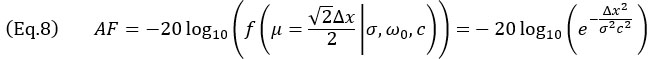
NDT 응용 분야의 일반적인 사용 사례인 AF 값이 작은 경우, AF에 대한 Δx의 값에 대한 대략적인 형태는 식 7의 진동 모델과

다음 식 8의 엔벨로프 모델에 대해 얻을 수 있습니다.
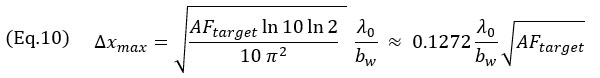
위 식은 모든 경우의 AF 값에 대한 그리드 크기의 제곱근 종속성을 변환합니다.식 9는 식 7의 2차 테일러 급수 근사치를 사용하여 도출한 것입니다.이 근사치는 정확한 모델과 함께 그림 6에 설명되어 있습니다.또한 진동 모델의 그리드 크기는 작은 bw의 상대 대역폭과 거의 무관합니다.진동 모델과 엔벨로프 모델 모두 최대 그리드 해상도 Δxmax가 목표한 진폭 충실도의 제곱근과 관련된다는 점도 언급할 만합니다.이러한 값은 현상학적 모델을 기반으로 코드를 준수하기 위한 최대 그리드 해상도를 나타냅니다.
(a) 진동 TFM에 대한 최악의 시나리오는 |
(b) TFM 엔벨로프에 대한 최악의 시나리오는 진폭 프로파일이 |
그림 5.(a) 진동 TFM, (b) TFM 엔벨로프의 경우 최악의 시나리오에 대한 그리드 직각 축에 대한 결함 방향 설명.
실험적 검증
제안된 모델은 세 가지 다른 TFM 검사 사용 사례에 대한 경험적 결과로 검증되었습니다.세 가지 TFM 설정 모두에 대해 다양한 그리드 해상도로 여러 SDH를 이미지화했으며 앞서 설명한 방법을 사용하여 진폭 충실도를 측정했습니다.세 가지 사용 사례의 매개변수는 표 1에 설명되어 있습니다.첫 번째 사례는 고주파 프로브(7.5MHz)와 접촉하고, 두 번째 사용 사례는 더 낮은 주파수(5MHz)의 횡파를 사용하며, 세 번째 사용 사례는 더 높은 프로브 주파수(10MHz)와 요소 수에서 횡파를 사용합니다.모든 사례에 대해 SDH는 탄소강 블록의 상단 표면에서 50mm 이내에 위치합니다.
표 1: 진폭 충실도 실험 검증에 사용되는 TFM 설정의 매개변수.
| 사례 | 프로브 매개변수 | 웨지 매개변수 | 부품 매개변수 | TFM 모드 | |||||
|---|---|---|---|---|---|---|---|---|---|
|
주파수
[MHz] |
번호
[#] |
피치
[mm] |
속도
[m/s] |
각도
[°] |
높이
[mm] |
속도
cp - cs [m/s] |
SDH
직경 [mm] | ||
| 1 | 7.5 | 64 | 1.0 | n/a | n/a | 0 | 3240 - 5890 | 1 | L-L |
| 2 | 5 | 32 | 1.0 | 2330 | 36.1 | 11.0 | 3240 - 5890 | 0.5 | T-T |
| 3 | 10 | 64 | 0.5 | 2330 | 36.1 | 11.0 | 3240 - 5890 | 1 | T-T |
그림 5는 표준 진동 TFM(상단)과 TFM 엔벨로프(하단)에 대한 진폭 충실도 결과를 보여줍니다.개별 회색 점은 각각 사용 사례, SDH, 그리드 해상도의 다양한 조합을 나타냅니다.앞에서 제시한 가우스 모델을 사용하여 추정한 진폭 충실도는 검은색 일반 곡선으로 표시합니다.빨간색 점선은 2dB의 코드 준수 한계를 나타냅니다.
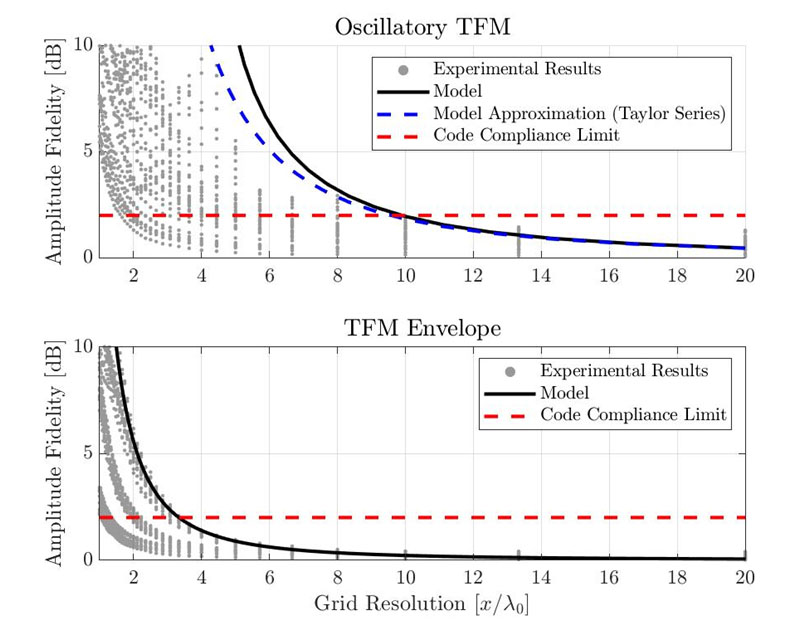
그림 6.표준 진동 TFM(상단)과 TFM 엔벨로프(하단)에 대한 경험적 방식의 진폭 충실도 측정과 제안된 가우스 모델 결과 사이의 비교.
제안된 모델에서 코드를 준수하는 데 필요한 해상도는 진동 TFM의 경우 λ0/9.9이고 TFM 엔벨로프의 경우 λ0/3.3입니다.실험 결과에 따르면 코드를 준수하기 위한 최소 그리드 해상도는 표준 진동 TFM의 경우 약 λ0/10이고 TFM 엔벨로프의 경우 λ0/3.3입니다.그러나 이러한 값은 제시된 실험적 사례의 최악의 경우에서 가져온 것입니다.측정한 진폭 충실도 값 중 일부는 그리드 해상도가 낮더라도 2dB 미만입니다.따라서 제안된 모델은 TFM 설정의 진폭 충실도에 대해 양호하면서도 보수적인 추정치를 제공합니다.
결론
TFM 설정의 진폭 충실도는 그리드 해상도와 관련하여 이미징의 견고함에 대한 중요한 척도입니다.그리드의 밀도가 높을수록 진폭 충실도 값이 낮아집니다.코드 및 표준에서는 이제 새로운 검사 기술로 TFM 방식을 포함하며 진폭 충실도는 2dB 이하로 요구됩니다.이 백서에서는 진폭 충실도를 경험적으로 올바르게 측정할 수 있는 방법을 제시하고 TFM 설정에 대한 결과인 진폭 충실도를 추정하기 위한 간단한 분석 모델을 제안합니다.
음향 전파의 주축을 따라 진폭 프로파일을 기반으로 간단한 분석 모델이 제안되었습니다.이 모델은 진폭 프로파일을 가우스 변조 코사인 진동으로 추정합니다.이 프로파일을 사용하여 진폭 충실도를 추정하면 표준 진동 TFM과 TFM 엔벨로프 모두에 대해 양호한 결과를 얻을 수 있습니다.경험적 결과는 표준 진동 TFM과 TFM 엔벨로프에 대해 각각 최대 λ0/10 또는 λ0/3.3의 그리드 해상도가 필요함을 보여주었습니다.제안된 분석 모델은 표준 TFM의 경우 λ0/9.9, TFM 엔벨로프의 경우 λ0/3.3의 그리드 해상도가 필요함을 추정합니다.따라서 제안된 모델은 TFM 설정의 진폭 충실도를 추정하는 데 사용할 수 있습니다.
코드 준수 솔루션의 일부로 TFM 엔벨로프를 사용할 때의 이점에 대해 자세히 알아보려면 백서 “엔벨로프 기능과 함께 TFM 사용”을 참조하십시오.
참고문헌
[1] ASME Committee, 2019, “ASME BPVC.V Article 4 Mandatory Appendix XI Full Matric Capture.”
[2] Oralkan, O.,Ergun, A.S.,Johnson, J.A.,Karaman, M.,Demirci, U.,Kaviani, K.,Lee, T.H.,Khuri-Yakub, B.T.,2002, “Capacitive Micromachined Ultrasonic Transducers: Next-Generation Arrays for Acoustic Imaging?,” IEEE Trans.Ultrason.,Ferroelect.,Freq.Contr.,49(11), pp.1596~1610.
[3] Thomenius, K.E.,1996, “Evolution of Ultrasound Beamformers,” 1996 IEEE Ultrasonics Symposium.Proceedings, IEEE, San Antonio, TX, USA, pp.1615~1622.
[4] Freeman, S.,Li, P.,O’Donnell, M.,“Retrospective Dynamic Transmit Focusing,” p.24.
[5] Wilcox, P.D.,2006, “Exploiting the Full Data Set from Ultrasonic Arrays by Post-Processing,” AIP Conference Proceedings, AIP, Brunswick, Maine (USA), pp.845~852.
[6] Portzgen, N.,Gisolf, D.,Blacquiere, G.,2007, “Inverse Wave Field Extrapolation: A Different NDI Approach to Imaging Defects,” IEEE Transactions on Ultrasonics, Ferroelectrics and Frequency Control, 54(1), pp.118~127.
[7] Sharpe, R.S.,ed.,1982, Research Techniques in Nondestructive Testing.Vol.6: ...,Acad.Press, London.
[8] Holmes, C.,Drinkwater, B.W.,Wilcox, P.D.,2008, “Advanced Post-Processing for Scanned Ultrasonic Arrays: Application to Defect Detection and Classification in Non-Destructive Evaluation,” Ultrasonics, 48(6~7), pp.636~642.
[9] Holmes, C.,Drinkwater, B.W.,Wilcox, P.D.,2005, “Post-Processing of the Full Matrix of Ultrasonic Transmit–Receive Array Data for Non-Destructive Evaluation,” NDT & E International, 38(8), pp.701~711.
[10] ISO, 2020, “ISO/DIS 23865 -FMC-TFM - General Use of TFM-FMC Technique.”
[11] Johnson, P.,2019, “With a New Software Wizard, There’s No Sorcery but the Magic of the M2M Gekko Is Evident with Instant Code Compliance for Your TFM Weld Inspections.,” Code Compliant TFM Weld Inspection with Three Clicks.
[12] ASME Committee, 2019, “ASME BPVC.V Article 4 Nonmandatory Appendix F - Examination of Welds Using Full Matrix Capture.”